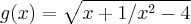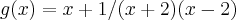por Soprano » Dom Set 25, 2016 17:25
por Soprano » Dom Set 25, 2016 17:25
Olá a todos,
Estou com dificuldade como conseguir descobrir o Domínio desta função:
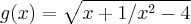
Sei que a função simplificada termina desta maneira:
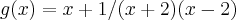
E sei que o domínio é representado desta maneira:
Df = ]-2,1] U ]2, +infinito[
Mas como sei que o domínio vai de dois para mais infinito? E não de menos infinito para 2?
Obrigado
-
Soprano
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Fev 14, 2016 10:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Electrónica
- Andamento: cursando
 por petras » Seg Dez 05, 2016 18:50
por petras » Seg Dez 05, 2016 18:50
Temos uma inequação quociente portanto é necessário analisar o quadro de sinais:
O que está dentro da raiz precisa ser positivo >=0
Lembrando que o denominador não pode ser 0, ou seja -2 e 2 não irão pertencer ao Domínio.
I) x - 1 ---> -----------------[-1]+++++++++++++++
II)x^2-4 --> +++++(-2)-------------------(2)+++++++
(I/II)------> -------(-2)+++++[-1]--------(2)+++++++
Portanto ]-2, 1] U ]2,+oo]
-
petras
- Usuário Parceiro

-
- Mensagens: 58
- Registrado em: Sex Jan 22, 2016 21:19
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Domínio] Determinar domínio a partir da função
por +danile10 » Qui Fev 07, 2013 21:33
- 1 Respostas
- 2886 Exibições
- Última mensagem por e8group

Qui Fev 07, 2013 22:38
Funções
-
- Como é o gráfico desta função, e qual o seu domínio?
por Ronaldobb » Qua Set 19, 2012 15:49
- 1 Respostas
- 1367 Exibições
- Última mensagem por MarceloFantini

Qua Set 19, 2012 22:58
Funções
-
- Determinar o domínio
por rodsales » Qui Jun 18, 2009 20:59
- 2 Respostas
- 3769 Exibições
- Última mensagem por rodsales

Sex Jun 19, 2009 20:58
Trigonometria
-
- [descobrir valor para domínio] Domínio da função
por Zebra-LNX » Sáb Jun 16, 2012 12:26
- 1 Respostas
- 3251 Exibições
- Última mensagem por MarceloFantini

Ter Jun 19, 2012 22:18
Funções
-
- Como posso Identificar o domínio ?
por Amanda j » Seg Out 24, 2016 12:57
- 0 Respostas
- 3670 Exibições
- Última mensagem por Amanda j

Seg Out 24, 2016 12:57
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.