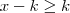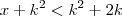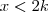Vou colocá-los aqui, e quem souber e me ajudar vou ser muito grato !
(Fuvest-SP) Qual é o conjunto solução da inequeação
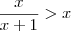 ?
?Agora, tem esse aqui. Eu sei que é fácil, tem uns 3 desse tipo, mas se eu conseguir resolver um consigo os demais.
(UFF-RJ) As empresas Alfa e Beta alugam televisores do mesmo tipo. A empresa Alfa cobra R$ 35,00 fixos pelos 30 primeiros dias de uso e R$ 1,00 por dia extra. A empresa Beta cobra R$ 15,00 pelos primeiros 20 dias de uso e R$ 1,50 por dia extra. Após N dias, o valor cobrado pela empresa Beta passa a ser maior que o do cobrado pela empresa Alfa. O valor de N é?
E este aqui meio chato.
(PUC-RJ) Seja K um número positivo. Então o conjunto dos números X tais que
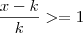 e
e 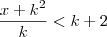 é?
é?Esse negócio de usar K no meio de inequações, não tenho idéia do que fazer!
Quem souber algum desses me ajuda ae por favor !
Muito obrigado!

Abrs


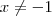 . Agora, multiplicando-se os dois lados por
. Agora, multiplicando-se os dois lados por  :
: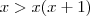
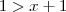
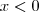
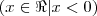
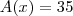 para
para 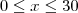 ;
;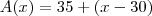 para
para 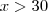
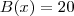 para
para 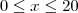
 para
para 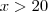
 , o custo é o mesmo. Em
, o custo é o mesmo. Em 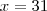 , o custo passa. Algebricamente:
, o custo passa. Algebricamente: para
para 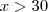
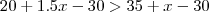
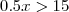
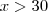
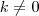 , multiplicando as duas desigualdades por
, multiplicando as duas desigualdades por  temos:
temos: