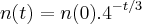
em que n(0) é a quantidade estimada de pássaros antes do início das construções e n(t) é a quantidade existente t anos depois.
Qual o tempo necessário para que a população de pássaros dessa espécie se reduza a:
a)à metade da população no início das construções?
b)à oitava parte da população no início das construções?
c) a 1,5625% da população no iníco das construções.
Eu consegui resolver o item a e o item b. O c não consegui resolver justamente devido à porcentagem.
Obrigado!


 (usando uma bem-vinda calculadora:)
(usando uma bem-vinda calculadora:)





