 por Lovegood » Qui Abr 02, 2015 08:25
por Lovegood » Qui Abr 02, 2015 08:25
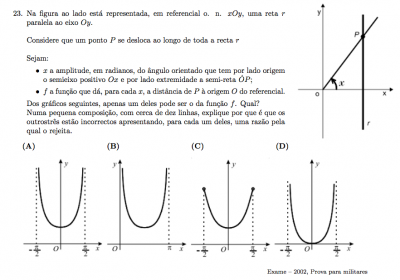
boa tarde alguém me ajuda a escolher o gráfico correto nesta questão. Estou na dúvida entre A e C...
Obrigado
- Anexos
-
-
Lovegood
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Set 29, 2013 09:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Baltuilhe » Qui Abr 02, 2015 16:43
por Baltuilhe » Qui Abr 02, 2015 16:43
Boa tarde!
Pela figura temos que um triângulo de base (do O até a reta r) de tamanho r.
Sua hipotenusa (já que é um triângulo retângulo) vale OP
A medida de OP pode ser obtida de:
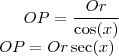
Sinal e valor da secante (1/cos) no x positivo;
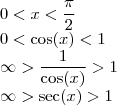
Mesmo para o lado negativo:
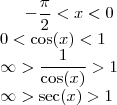
Então, o valor de y vai de 1 * r = r a infinito, tanto para x positivo quanto para x negativo.
Resposta: letra a)
Espero ter ajudado!
-
Baltuilhe
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Dom Mar 24, 2013 21:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [FUNÇÕES]ESTÁ CORRETO ISSO?
por Miya » Seg Mar 30, 2015 10:14
- 1 Respostas
- 840 Exibições
- Última mensagem por adauto martins

Seg Mar 30, 2015 21:30
Funções
-
- Grafico de funções
por proluxe » Sex Ago 22, 2008 00:39
- 1 Respostas
- 2920 Exibições
- Última mensagem por admin

Sex Ago 22, 2008 01:02
Trigonometria
-
- Gráfico de Funções
por GabyRitter » Dom Mai 17, 2009 19:29
- 2 Respostas
- 1973 Exibições
- Última mensagem por gwirith

Dom Mai 17, 2009 20:51
Funções
-
- Gráfico das Funções
por Luna » Sáb Set 12, 2009 17:41
- 1 Respostas
- 1352 Exibições
- Última mensagem por Elcioschin

Dom Set 13, 2009 21:19
Funções
-
- Grafico de funções
por Thassya » Qua Out 20, 2010 17:40
- 2 Respostas
- 1936 Exibições
- Última mensagem por MarceloFantini

Qua Out 20, 2010 20:53
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



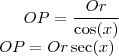
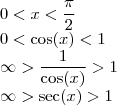
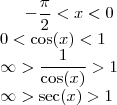



 , avisa que eu resolvo.
, avisa que eu resolvo.

