Oi,
Gostaria de solicitar a vossa ajuda para calcular as raízes de uma função, conforme o exercício em anexo. Qual o melhor metodo para este cálculo?
Obrigado
por EREGON » Sex Nov 14, 2014 14:22
por EREGON » Sex Jan 16, 2015 11:04
por adauto martins » Seg Jan 19, 2015 09:56
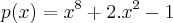
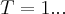(++-)uma troca de sinal,entao 
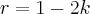,como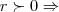 
tem uma raiz real positiva...
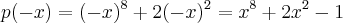...logo 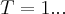,pois(++-),uma troca de sinais...
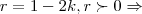,p(x) tera uma raiz real negativa...entao pode-se concluir q. p(x) tem uma raiz real positiva,uma raiz real negativa e tres raizes complexas e seus conjugados,pois sua ordem e de 8...junto a soluçao segue um anexo sobre raizes de polinomios
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)