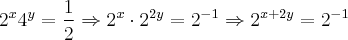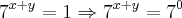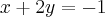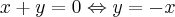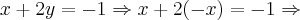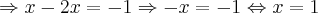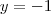Matheus,
Vamos alterar o sistema para valores semelhantes elevados à potências que podem ser diferentes, ou seja:
Da primeira equação tiramos que:
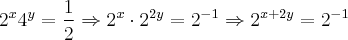
Da segunda equação obtemos:
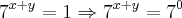
Das duas últimas equações, como as bases são iguais em ambos os lados da equação, podemos dizer que:
[A]
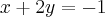
[B]
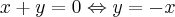
Usando este último resultado [B] na primeira equação [A], teremos:
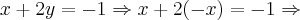
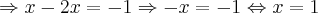
Usando este resultado em [B] no qual já sabemos que y = -x, obtemos que:
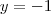
Que são os valores que desejávamos obter.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali