Equações cartesianas e equações paramétricas

[Victor Mello]

Boa tarde, eu estou tentando resolver uma questão que pedia para identificar a trajetória da partícula encontrando a equação cartesiana para ela a partir da equação paramétrica x=cos2t, y=sen2t, cujo intervalo de t varia de .

Pois bem, eu fiz uma substituição através de 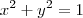nas equações paramétricas. O problema foi na hora de identificar a trajetória da partícula: quando igualei t a 0, então x=1 e y=0. E quando igualei t a pi, o x também é igual a 1, e y também é zero, ou seja, a medida que aumento o t até fechar o intervalo, eu obtive o mesmo ponto que a partícula deve percorrer, ou seja, ele parte de um ponto, e depois ela volta para o mesmo ponto. E eu não tenho muita certeza se isso está correto ou não. Poderia alguém me explicar a lógica dessa questão? Enfim, quem puder, eu agradeço!

Abraço!

[Russman]

Ta certo. A partícula descreve uma circunferência completa! A partícula parte do ponto (1,0) e, após descrever uma circunferência de raio 1 em torno da origem, retorna ao ponto (1,0).