Qual o domínio da seguinte função f(x) =³?x+2/x-3
Peço desculpas,por não conseguir formatar no Latex



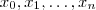 , daí o domínio da função será o complementar de
, daí o domínio da função será o complementar de 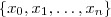 .
. 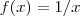 , temos q esta função f está bem definida sempre que
, temos q esta função f está bem definida sempre que  .Portanto , para qualquer
.Portanto , para qualquer 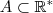 não vazio , podemos definir
não vazio , podemos definir 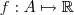 que associa a cada
que associa a cada  em
em  a um número
a um número 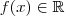 .Logicamente , o maior subconjunto de
.Logicamente , o maior subconjunto de 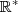 é o próprio
é o próprio 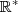 ...
...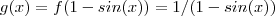 .Encontrar o domínio de g não é tão trivial , mas não tão difícil assim ...
.Encontrar o domínio de g não é tão trivial , mas não tão difícil assim ...  não estar definido . Isto ocorre quando
não estar definido . Isto ocorre quando 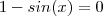 ou seja quando
ou seja quando 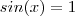 .Temos que
.Temos que 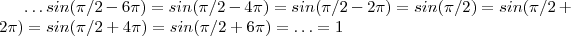
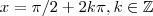 ... O maior domínio possível é
... O maior domínio possível é 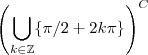 , em outras palavras , o conjunto dos números reais tirando os infinitos pontos que se exprimir por
, em outras palavras , o conjunto dos números reais tirando os infinitos pontos que se exprimir por 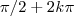 com
com  inteiro .
inteiro .
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.