 por Maria Tamires » Qui Jul 11, 2013 10:17
por Maria Tamires » Qui Jul 11, 2013 10:17
Estou com muita dificuldade para resolver esse exercício
Se
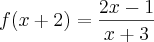
,
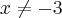
, o domínio de f(x) é:
a) R
b) R*
c) {
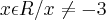
d)
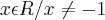
e)
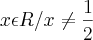
Resolução
g(x)=x+2 -> f(y) -> y=x+2
![f\left[g(x) \right]=\frac{2x-1}{x+3} => \frac{2y-1}{y+3} =>\frac{2(x+2)-1}{x+2+3} => \frac{2x+4-1}{x+5} => \frac{2x+3}{x+5} f\left[g(x) \right]=\frac{2x-1}{x+3} => \frac{2y-1}{y+3} =>\frac{2(x+2)-1}{x+2+3} => \frac{2x+4-1}{x+5} => \frac{2x+3}{x+5}](/latexrender/pictures/c2cf91149454a9be572e5453ffbde51b.png)
Parei aí... não consigo terminar pois não sei como acha a restrição para o numerador! Me ajude por favor...
-
Maria Tamires
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jul 11, 2013 09:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3°
- Andamento: cursando
 por timoteo » Qui Jul 11, 2013 12:12
por timoteo » Qui Jul 11, 2013 12:12
Olá Tamires.
A questão pede o domínio de f(x) e este é igual a imagem de g(x). Sabendo disso qual é a imagem de g(x)?
Resposta: Im g(x) = R.
Estimas!
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por Maria Tamires » Qui Jul 11, 2013 13:15
por Maria Tamires » Qui Jul 11, 2013 13:15
poxa eu também pensei assim... só que meu prof falo que é a alternativa d!!
-
Maria Tamires
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jul 11, 2013 09:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3°
- Andamento: cursando
 por timoteo » Qui Jul 11, 2013 14:14
por timoteo » Qui Jul 11, 2013 14:14
Esqueci de colocar que temos que levar a condição de existência de f(x) em consideração, então com f(x) =
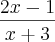
, a condição pede x =/= -3. Portando na minha opinião a letra correta é a C.
Caso você tenha a resposta dele você posta ai!
Estimas!
P.S. Vamos ver se alguém tem outra opinião.
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por Maria Tamires » Qui Jul 11, 2013 14:32
por Maria Tamires » Qui Jul 11, 2013 14:32
Obrigada
Quando ele posta a resolução imediatamente posto aqui!
-
Maria Tamires
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jul 11, 2013 09:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3°
- Andamento: cursando
 por Maria Tamires » Sex Jul 12, 2013 11:56
por Maria Tamires » Sex Jul 12, 2013 11:56
Consegui chegar no resultado
realmente é a alternativa D
-
Maria Tamires
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jul 11, 2013 09:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3°
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função composta]Achar o dominio de uma função composta
por lucasmath » Dom Abr 12, 2015 16:09
- 0 Respostas
- 2234 Exibições
- Última mensagem por lucasmath

Dom Abr 12, 2015 16:09
Funções
-
- [FUNÇÃO] NAO CONSIGO ENTENDER FUNÇÃO COMPOSTA!
por Gabriela AlmeidaS » Seg Mai 12, 2014 19:18
- 5 Respostas
- 5465 Exibições
- Última mensagem por Toussantt

Dom Jan 24, 2016 15:34
Funções
-
- Função composta
por scorpion » Sáb Out 25, 2008 11:09
- 2 Respostas
- 4203 Exibições
- Última mensagem por scorpion

Qua Out 29, 2008 14:26
Funções
-
- Função Composta
 por ginrj » Ter Jun 30, 2009 17:35
por ginrj » Ter Jun 30, 2009 17:35
- 4 Respostas
- 17049 Exibições
- Última mensagem por LuizAquino

Sáb Mar 03, 2012 14:34
Funções
-
- Função composta
 por matemalouco » Sáb Ago 15, 2009 20:43
por matemalouco » Sáb Ago 15, 2009 20:43
- 2 Respostas
- 3986 Exibições
- Última mensagem por Elcioschin

Seg Ago 17, 2009 10:26
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
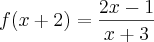 ,
, 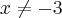 , o domínio de f(x) é:
, o domínio de f(x) é: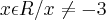
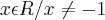
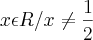
![f\left[g(x) \right]=\frac{2x-1}{x+3} => \frac{2y-1}{y+3} =>\frac{2(x+2)-1}{x+2+3} => \frac{2x+4-1}{x+5} => \frac{2x+3}{x+5} f\left[g(x) \right]=\frac{2x-1}{x+3} => \frac{2y-1}{y+3} =>\frac{2(x+2)-1}{x+2+3} => \frac{2x+4-1}{x+5} => \frac{2x+3}{x+5}](/latexrender/pictures/c2cf91149454a9be572e5453ffbde51b.png)

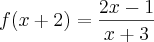 ,
, 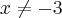 , o domínio de f(x) é:
, o domínio de f(x) é: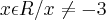
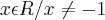
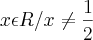
![f\left[g(x) \right]=\frac{2x-1}{x+3} => \frac{2y-1}{y+3} =>\frac{2(x+2)-1}{x+2+3} => \frac{2x+4-1}{x+5} => \frac{2x+3}{x+5} f\left[g(x) \right]=\frac{2x-1}{x+3} => \frac{2y-1}{y+3} =>\frac{2(x+2)-1}{x+2+3} => \frac{2x+4-1}{x+5} => \frac{2x+3}{x+5}](/latexrender/pictures/c2cf91149454a9be572e5453ffbde51b.png)



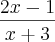 , a condição pede x =/= -3. Portando na minha opinião a letra correta é a C.
, a condição pede x =/= -3. Portando na minha opinião a letra correta é a C.


