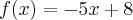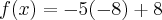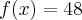por Luanna » Ter Nov 10, 2009 15:34
por Luanna » Ter Nov 10, 2009 15:34
1 ) Através de um estudo sobre o consumo de energia elétrica de uma fábrica , chegou-se é equação C= 400t , em que C é o consumo em KW/h e t é o tempo em dias. Quantos dias são necessários para que o consumo atinja 4800 KW/h ?
2 )Dada a função f: R -> R definida por f(x)= -5 + 8 , determine f(-8) .
-
Luanna
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Nov 10, 2009 15:26
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Cleyson007 » Ter Nov 10, 2009 18:27
por Cleyson007 » Ter Nov 10, 2009 18:27
Boa tarde Luanna!
Primeiramente, seja bem vinda ao Ajuda Matemática!
Quanto ao exercício 01 -->
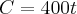
Para descobrir o tempo em dias, basta substituir o valor de
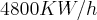
em C, veja só:


Resolvendo,
 São necessários 12 dias para que o consumo atinja 4800 KW/h.
São necessários 12 dias para que o consumo atinja 4800 KW/h.Quanto ao exercício 02 --> Luanna, favor conferir o enunciado da questão, ok?
Comente qualquer dúvida

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Luanna » Ter Nov 10, 2009 19:43
por Luanna » Ter Nov 10, 2009 19:43
Muito obrigada Cleyson007 por ter me ajudado ! Agora a questão 2 , eu a escrevi do mesmo jeito que esta aqui no meu exercicio ! mas tudo bem.....vou tentando fazer !
-
Luanna
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Nov 10, 2009 15:26
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Cleyson007 » Qua Nov 11, 2009 13:34
por Cleyson007 » Qua Nov 11, 2009 13:34
Luanna escreveu:Muito obrigada Cleyson007 por ter me ajudado ! Agora a questão 2 , eu a escrevi do mesmo jeito que esta aqui no meu exercicio ! mas tudo bem.....vou tentando fazer !
Boa tarde Luanna!
Luanna, a função do 1º grau é escrita na forma
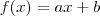
.
No seu exercício, o que deve ser feito é substituir o valor de x por -8. Repare que a função digitada não apresenta o valor de x (f(x)= -5 + 8)..
Se fosse, por exemplo:
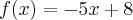
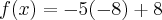
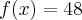
Comente qualquer dúvida

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função] isso é função do segundo grau?
por maulakalanata » Qua Mar 27, 2013 04:03
- 1 Respostas
- 2289 Exibições
- Última mensagem por timoteo

Qua Mar 27, 2013 10:51
Funções
-
- [Função 1°grau] determinar função.
por Thiago 86 » Ter Abr 23, 2013 11:27
- 2 Respostas
- 2412 Exibições
- Última mensagem por Thiago 86

Ter Abr 23, 2013 13:05
Funções
-
- Função do 2° Grau
por mimi2009 » Qua Jun 10, 2009 05:46
- 1 Respostas
- 2093 Exibições
- Última mensagem por Molina

Qua Jun 10, 2009 08:05
Funções
-
- Função do 2 grau...
por Fiel8 » Qua Jul 01, 2009 21:34
- 4 Respostas
- 3448 Exibições
- Última mensagem por Cleyson007

Qui Jul 02, 2009 16:16
Funções
-
- Função 1° grau
por DanielFerreira » Ter Set 22, 2009 14:14
- 2 Respostas
- 2145 Exibições
- Última mensagem por DanielFerreira

Ter Set 22, 2009 19:06
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


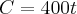
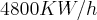 em C, veja só:
em C, veja só: 





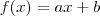 .
.