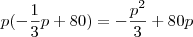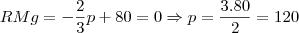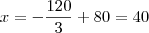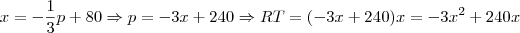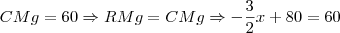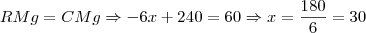por jason013 » Dom Jun 02, 2013 22:38
por jason013 » Dom Jun 02, 2013 22:38
Prezados,
Estou encontrando dificuldades de interpretar e resolver a seguinte questão.
Dada a função demanda x= -1/3p + 80 e a função custo total C(x)= 60x +150.
a) Obtenha o valor de x que maximiza a receita.
b) Obtenha L(x);
c) Obtenha o valor de x que maximiza o lucro.
d) Obtenha L(p);
e) Qual deve ser o preço para o lucro ser máximo?
Grato pessoal..
-
jason013
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Jun 02, 2013 22:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Contábeis
- Andamento: cursando
 por temujin » Seg Jun 03, 2013 13:41
por temujin » Seg Jun 03, 2013 13:41
Sugiro que vc escreva as funções e aí faça a maximização:
a) Receita é dada por p.x:
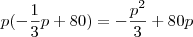
Para maximizar, vc precisa encontrar os pontos críticos e testar se é mínimo ou máximo. Pela forma da função, fica claro que será um máximo (é uma parábola côncava). Derivando e igualando a zero (ou seja, achando a função receita marginal):
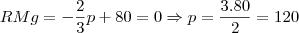
Basta resolver para p e substituir na equação de demanda:
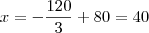
b) Lucro é RT - CT.
Basta substituir os valores de x: px - c(x) = 120.40 - 60.40-150 = 2250
c) A condição de lucro máximo é quando a RMg é igual ao CMg. Reescreva RMg em função de x.
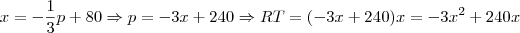

Para obter o custo marginal, da mesma forma que a receita, derive e iguale a zero a função custo. Aí basta igualar as duas funções e resolver para x:
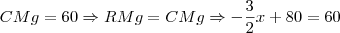
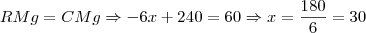
Com isso acho que dá pra concluir, certo?
-
temujin
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- como resolver essa função
por kzacristo19 » Seg Ago 26, 2013 16:43
- 0 Respostas
- 1001 Exibições
- Última mensagem por kzacristo19

Seg Ago 26, 2013 16:43
Funções
-
- Função quadrática
por Ananda » Sex Mar 28, 2008 16:00
- 6 Respostas
- 9243 Exibições
- Última mensagem por admin

Sex Mar 28, 2008 21:25
Funções
-
- Função quadratica
por Aline » Qui Jun 18, 2009 14:22
- 2 Respostas
- 2634 Exibições
- Última mensagem por Cleyson007

Sex Jun 19, 2009 10:00
Funções
-
- Função Quadratica
por Aline » Qui Jun 18, 2009 14:37
- 1 Respostas
- 2018 Exibições
- Última mensagem por Marcampucio

Qui Jun 18, 2009 16:45
Funções
-
- Função Quadratica
por Aline » Sáb Jun 20, 2009 18:23
- 1 Respostas
- 2097 Exibições
- Última mensagem por Molina

Dom Jun 21, 2009 20:28
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.