![\sqrt[2]{\frac{x}{x+1}} \sqrt[2]{\frac{x}{x+1}}](/latexrender/pictures/6054963843119414615105f21e5e7a92.png) na resposta do livro é: (-infinito, -1) U [0,+infinito), não consegui chegar a essa resposta consegui encontrar apenas o -1, pois x+1#0, logo x#-1, porem como fica
na resposta do livro é: (-infinito, -1) U [0,+infinito), não consegui chegar a essa resposta consegui encontrar apenas o -1, pois x+1#0, logo x#-1, porem como fica 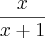 > ou igual a zero??? eu achei x-x>=1. Como fica isso?
> ou igual a zero??? eu achei x-x>=1. Como fica isso?
![\sqrt[2]{\frac{x}{x+1}} \sqrt[2]{\frac{x}{x+1}}](/latexrender/pictures/6054963843119414615105f21e5e7a92.png) na resposta do livro é: (-infinito, -1) U [0,+infinito), não consegui chegar a essa resposta consegui encontrar apenas o -1, pois x+1#0, logo x#-1, porem como fica
na resposta do livro é: (-infinito, -1) U [0,+infinito), não consegui chegar a essa resposta consegui encontrar apenas o -1, pois x+1#0, logo x#-1, porem como fica 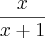 > ou igual a zero??? eu achei x-x>=1. Como fica isso?
> ou igual a zero??? eu achei x-x>=1. Como fica isso?
 , uma vez que, a restrição imposta foi apenas que
, uma vez que, a restrição imposta foi apenas que  . E isso não está correto! Como disse anteriormente, se o índice da raiz é par, então o radicando não pode ser negativo!
. E isso não está correto! Como disse anteriormente, se o índice da raiz é par, então o radicando não pode ser negativo!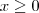

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)