 por Jovilaco » Qui Mar 14, 2013 21:20
por Jovilaco » Qui Mar 14, 2013 21:20
Olá estou com dúvida sobre estes exercícios o professor passou no quadro e não consegui resolve-los. ALém do mais gostaria que alguém me indicasse o que estudar(matérias) para ir melhor nesses tipos de exercícios(levantamento de indeterminações) muito obrigado!
Lim x?0 ((?16 ?x) ?4)/x
Lim h?0 ((a + h)3 ?a3)/h
-
Jovilaco
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Mar 14, 2013 21:12
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qui Mar 14, 2013 22:07
por e8group » Qui Mar 14, 2013 22:07
Por favor sempre utilize LaTeX para redigir suas expressões.Além disso ,seria importante postar apenas uma dúvida por tópico .
Observe o código e o resultado [(1),(2)]:
- Código: Selecionar todos
\lim_{x\to 0} \frac{\sqrt{16-x} - 4 }{x}
(1)
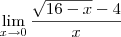
- Código: Selecionar todos
\lim_{h\to 0} \frac{(a+h)^3 - a^3 }{h}
(2)
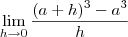
Resolução :
Em (1) ,basta multiplicar o numerador e o denominador por

. Fazendo as devidas simplificações e calculando o limite encontrará a resposta desejada .(Observe
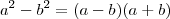
e também
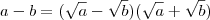
neste caso desde que
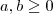
,no outro não há restrição )
Em(2) ,uma das possíveis formas de solução é considerar
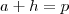
.Assim , quando
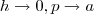
.
Deste modo, este limite é equivalente a
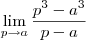
.
Mas ,

pode ser fatorado ,isto é ,
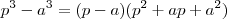
.
Então ,
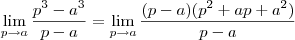
,visto que
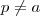
,ou seja,
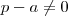
podemos simplificar a expressão acima ,obtendo
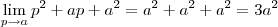
.
Portanto , podemos dizer que
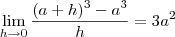
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda Urgente
por Mimizinha » Qua Mar 19, 2008 16:45
- 2 Respostas
- 6262 Exibições
- Última mensagem por XILVANA

Qui Abr 11, 2013 13:58
Álgebra Elementar
-
- ajuda urgente
por pedro ferreira » Seg Ago 24, 2009 22:53
- 2 Respostas
- 6080 Exibições
- Última mensagem por pedro ferreira

Seg Ago 24, 2009 23:08
Funções
-
- ajuda urgente!
por Fabricio dalla » Qua Jun 01, 2011 16:29
- 2 Respostas
- 2297 Exibições
- Última mensagem por Claudin

Qua Jun 01, 2011 20:14
Funções
-
- AJUDA URGENTE
por kersiafiorio » Qua Mar 21, 2012 15:59
- 1 Respostas
- 1705 Exibições
- Última mensagem por DanielFerreira

Qui Mar 22, 2012 01:26
Funções
-
- [URGENTE] AJUDA
por santtus » Sex Fev 08, 2013 02:57
- 3 Respostas
- 2356 Exibições
- Última mensagem por DanielFerreira

Ter Fev 12, 2013 13:01
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


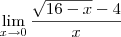
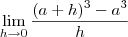
 . Fazendo as devidas simplificações e calculando o limite encontrará a resposta desejada .(Observe
. Fazendo as devidas simplificações e calculando o limite encontrará a resposta desejada .(Observe 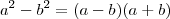 e também
e também 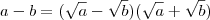 neste caso desde que
neste caso desde que 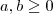 ,no outro não há restrição )
,no outro não há restrição )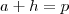 .Assim , quando
.Assim , quando 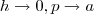 .
.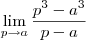 .
.  pode ser fatorado ,isto é ,
pode ser fatorado ,isto é , 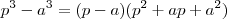 .
. 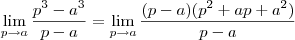 ,visto que
,visto que 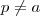 ,ou seja,
,ou seja, 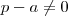 podemos simplificar a expressão acima ,obtendo
podemos simplificar a expressão acima ,obtendo 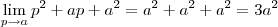 .
. 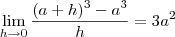 .
.


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.