 por Danilo » Dom Mar 10, 2013 15:50
por Danilo » Dom Mar 10, 2013 15:50
Construir o gráfico da função real:
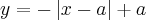
Bom, eu consigo fazer usando a definição de módulo normalmente, mas eu não sei como proceder utilizando somente variáveis. Grato a quem puder ajudar !
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Dom Mar 10, 2013 16:49
por e8group » Dom Mar 10, 2013 16:49
Boa tarde . Observe que

sempre será positivo ou nulo quando

.
Para qualquer

real ,vale que ,
1)
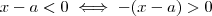
e ainda
![x-a< 0 \iff (x-a) + a = x +[a +(-a)] = x < a \iff -x >-a x-a< 0 \iff (x-a) + a = x +[a +(-a)] = x < a \iff -x >-a](/latexrender/pictures/8d4b0a609e577b69ad5152edf86377c6.png)
2)
![x -a \geq 0 \iff x + [a +(-a)] > 0 + a \iff x \geq a x -a \geq 0 \iff x + [a +(-a)] > 0 + a \iff x \geq a](/latexrender/pictures/7df5c72b92fd62b71d1295959b3e6f40.png)
Ficou claro ? Se não ,recomendo que verifique para
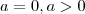
e
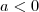
.
De 1) e 2) segue
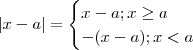
.
Assim ,
![y = -|x-a| + a = \begin{cases} -(x - a) + a ; x \geq a \\ -[-(x-a)] +a ; x < a \end{cases} y = -|x-a| + a = \begin{cases} -(x - a) + a ; x \geq a \\ -[-(x-a)] +a ; x < a \end{cases}](/latexrender/pictures/fdd8cce801cad5f0e86bdc6e5356a654.png)
Simplificando , obtemos :
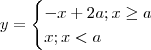
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função Modular - dúvida
por jamiel » Qui Abr 28, 2011 13:11
- 18 Respostas
- 15506 Exibições
- Última mensagem por jamiel

Qui Mai 05, 2011 14:08
Funções
-
- Dúvida (derivada e função modular)
 por Man Utd » Sáb Jun 15, 2013 11:03
por Man Utd » Sáb Jun 15, 2013 11:03
- 5 Respostas
- 7680 Exibições
- Última mensagem por LuizAquino

Dom Jun 16, 2013 11:24
Cálculo: Limites, Derivadas e Integrais
-
- [Função modular] Dúvida com relação a raízes
por exburro » Sáb Mar 31, 2012 01:23
- 1 Respostas
- 2599 Exibições
- Última mensagem por LuizAquino

Sex Abr 06, 2012 12:40
Funções
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7397 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
-
- Inequação Modular (Dúvida)
 por renanrdaros » Ter Mar 22, 2011 23:33
por renanrdaros » Ter Mar 22, 2011 23:33
- 13 Respostas
- 11562 Exibições
- Última mensagem por renanrdaros

Qua Mar 23, 2011 17:36
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
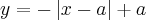

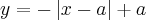

 sempre será positivo ou nulo quando
sempre será positivo ou nulo quando  .
. real ,vale que ,
real ,vale que , 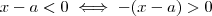 e ainda
e ainda ![x-a< 0 \iff (x-a) + a = x +[a +(-a)] = x < a \iff -x >-a x-a< 0 \iff (x-a) + a = x +[a +(-a)] = x < a \iff -x >-a](/latexrender/pictures/8d4b0a609e577b69ad5152edf86377c6.png)
![x -a \geq 0 \iff x + [a +(-a)] > 0 + a \iff x \geq a x -a \geq 0 \iff x + [a +(-a)] > 0 + a \iff x \geq a](/latexrender/pictures/7df5c72b92fd62b71d1295959b3e6f40.png)
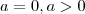 e
e 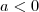 .
. .
. ![y = -|x-a| + a = \begin{cases} -(x - a) + a ; x \geq a \\ -[-(x-a)] +a ; x < a \end{cases} y = -|x-a| + a = \begin{cases} -(x - a) + a ; x \geq a \\ -[-(x-a)] +a ; x < a \end{cases}](/latexrender/pictures/fdd8cce801cad5f0e86bdc6e5356a654.png)
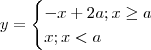


 .
.



