 por SILMARAKNETSCH » Sex Nov 09, 2012 15:29
por SILMARAKNETSCH » Sex Nov 09, 2012 15:29
F (X) = 2X² - 3X -2
DETERMINE A DERIVADA DESSA FUNÇÃO PARA QUALQUER X0 QUE PERTENÇA AO SEU DOMÍNIO. A SEGUIR CALCULE F' (5)
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
 por SILMARAKNETSCH » Sex Nov 09, 2012 15:42
por SILMARAKNETSCH » Sex Nov 09, 2012 15:42
CALCULE f" (5 ) ok
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
 por e8group » Sex Nov 09, 2012 16:03
por e8group » Sex Nov 09, 2012 16:03
Olá , a primeira coisa que vc dever fazer é estabelecer a derivada , logo após , vc calculará a derivada , neste caso f'(5) .
Eu suponho que conheça as regras que usamos para derivar , caso tenha alguma dúvida só postar algo .
Deivada de

é ,

pois ,
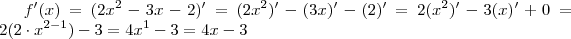
.
Daí ,
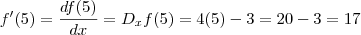
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por SILMARAKNETSCH » Sex Nov 09, 2012 16:08
por SILMARAKNETSCH » Sex Nov 09, 2012 16:08
eu vergonhosamente não sei a regra da derivação não sei chegar ao resultado derivado se não for passo a passo é isso que esta me faltando eu não sei o básico
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
 por e8group » Sex Nov 09, 2012 16:41
por e8group » Sex Nov 09, 2012 16:41
Compreendo . Bom quando eu comecei a estudar matemática do ens.médio , ao invés de eu fazer os exercícios do livro eu refazia os exemplos antes de eu ver a solução proposta pelo livro , Talvez se vc conseguir exercícios com resolução completa e tentar fazê-los ,conseguirá um desempenho melhor , matemática é esforço . O aprendizado de cálculo 1 estar relacionado também com o conhecimento de matemática do ensino fundamental e médio , principalmente funções . No youtube há aulas de cálculo que pode ajudar , uma delas é do Professor Luis Aquino , endereço :
http://www.youtube.com/user/LCMAquino
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por SILMARAKNETSCH » Sex Nov 09, 2012 16:50
por SILMARAKNETSCH » Sex Nov 09, 2012 16:50
vou sim ver esta aula eu tive problemas com contabilidade e tirei média 7 na prova estudando tudo por vídeo que foram me indicando, agradeço sua colaboração e se quiser saber mais da minha luta entre no meu site
www.docespimentas.com.br tem minha história um pouquinho depois do meu acidente estou concretizando um sonho de fazer a faculdade mesmo porque fiquei df e terei que ter uma empresa minha, ando mas nunca mais como antes, mas a vida é para vencermos obstáculos e estou tentando por todos os lados que acho enquanto não posso exatamente voltar ao mundo ai fora normal. estudo EAD no claretiano.
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4592 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- [Função] Dada a função, determine as constantes
por Raphael Leal » Qua Abr 02, 2014 16:42
- 1 Respostas
- 2359 Exibições
- Última mensagem por rodrigorc

Qua Abr 02, 2014 18:13
Funções
-
- [Função] Dada a função determine as Coordenadas
por Raphael Leal » Qui Abr 03, 2014 11:12
- 1 Respostas
- 1291 Exibições
- Última mensagem por rodrigorc

Qui Abr 03, 2014 17:57
Funções
-
- Dada uma função, calcular os zeros
por Tixa11 » Sáb Nov 10, 2012 12:26
- 4 Respostas
- 2960 Exibições
- Última mensagem por Tixa11

Seg Nov 12, 2012 18:05
Funções
-
- Investigue o comportamento da funçaõ dada f(x)
por Ana Maria da Silva » Sex Mai 17, 2013 11:52
- 0 Respostas
- 1163 Exibições
- Última mensagem por Ana Maria da Silva

Sex Mai 17, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 é ,
é ,  pois ,
pois , 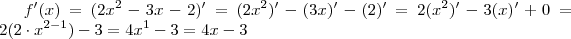 .
.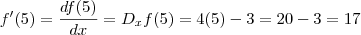 .
.








