 por Ronaldobb » Qui Set 20, 2012 19:25
por Ronaldobb » Qui Set 20, 2012 19:25
As questões a seguir referem-se ao gráfico abaixo.
http://i.imgur.com/BUisE.pnga) O ponto ( 1000, 4000) está no gráfico da função C(x). Traduza esta afirmação matemática em termos da função custo.
b) Qual é a variável independente?
c) Expresse com palavras as questões matemáticas: ' encontre o valor de "x" para o qual C(x) = 3500' ; 'encontre C(400)'.
d) Suponha que 500 unidades do produto são produzidas. Qual é o custo para produzir 100 unidades a mais?
-
Ronaldobb
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Ter Set 18, 2012 19:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por MarceloFantini » Qui Set 20, 2012 21:29
por MarceloFantini » Qui Set 20, 2012 21:29
Se o gráfico representa a função custo, então isto significa que
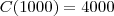
. A variável independente é

. Queremos encontrar o número de peças tal que o custo seja de 3500 e encontre o custo de 400 peças. O custo para produzir 100 unidades a mais será o custo de 600 unidades menos o custo de 500 unidades.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como eu resolvo essa questão
por diegoconain5 » Qua Jul 16, 2014 18:53
- 0 Respostas
- 1203 Exibições
- Última mensagem por diegoconain5

Qua Jul 16, 2014 18:53
Equações
-
- Como resolvo essa função? ALGUÉM SABE?
por Kelvin Brayan » Qua Mai 25, 2011 13:12
- 3 Respostas
- 2764 Exibições
- Última mensagem por Kelvin Brayan

Qui Mai 26, 2011 10:58
Funções
-
- Como resolvo essa equação?
por LuizCarlos » Seg Jul 25, 2011 14:07
- 8 Respostas
- 4954 Exibições
- Última mensagem por LuizCarlos

Ter Jul 26, 2011 00:04
Sistemas de Equações
-
- Ajudem-me. Como resolvo essa matriz.?
por danielvale28 » Ter Ago 11, 2009 08:55
- 2 Respostas
- 2499 Exibições
- Última mensagem por Cleyson007

Ter Ago 11, 2009 15:57
Matrizes e Determinantes
-
- Como resolvo essa integral indefinida??
por Justiceira » Sáb Out 31, 2009 19:52
- 3 Respostas
- 3075 Exibições
- Última mensagem por Molina

Seg Nov 23, 2009 21:06
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


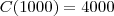 . A variável independente é
. A variável independente é  . Queremos encontrar o número de peças tal que o custo seja de 3500 e encontre o custo de 400 peças. O custo para produzir 100 unidades a mais será o custo de 600 unidades menos o custo de 500 unidades.
. Queremos encontrar o número de peças tal que o custo seja de 3500 e encontre o custo de 400 peças. O custo para produzir 100 unidades a mais será o custo de 600 unidades menos o custo de 500 unidades.


 .
.



