Primeiramente me desculpa faço parte do grupo a pouco tempo e ainda não sei mexer direito , por isso não sei se coloquei a minha duvida no lugar certo . Eu to estudando pro concurso as matemática to mt dificuldades , peço q me ajude . Nao consegui resolver esse problema , tentei de tudo mas nd bate na resposta certa.
Paulo aplicou no Banco Postal, um capital de R$ 100,00, a uma taxa de juros simples de t% ao ano. Os juros obtidos
após um ano, foram aplicados à mesma taxa de juros simples de t% ao ano, durante mais um ano. Se o juro total foi
de R$ 17,25, qual a taxa de juros simples anual que Paulo aplicou seu dinheiro?
Gabarito D) 15% a.a.
Espero q vc's possa me ajudar . Juros , Porcentagem e Fração é meu ponto fraco . Desde já obrigada



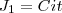
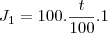
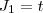 reais.
reais.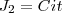
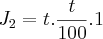
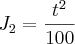

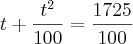

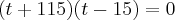
 ,
,

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
