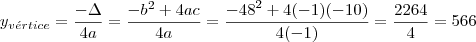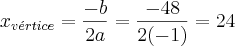por Larice Mourao » Qua Mai 30, 2012 12:08
por Larice Mourao » Qua Mai 30, 2012 12:08
Então , eu pesquisei no site , mas não encontrei essa questão que é da UFT , e eu vou prestar vestibular domingo (03/05) , se alguém puder me orientar até sexta - hehe - fico extremamente grata !
Uma empresa do ramo de confecções produz e
comercializa calças jeans. Se x representa a quantidade
produzida e comercializada (em milhares de unidades) e
l(x) = - x² + 48x - 10
representa o lucro (em milhares de reais) da empresa para
x unidades, então o lucro máximo que a empresa poderá
obter é:
Eu vi na internet uma resposta usando limite , eu acho, mas não sei o que é isso ..
então tentei substituir o '' l(x) '' por ''y'' aí isolei o Y e substituí no lugar do x , mas não ta dando certo , tentei fazer por Báskara , mas não é um trinômio quadrado perfeito .. o que eu devo fazer a nível de Ensino Médio ?
-
Larice Mourao
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Mai 17, 2012 15:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Qua Mai 30, 2012 14:37
por Russman » Qua Mai 30, 2012 14:37
A nível de Ensino Médio, você deve perceber que a função
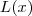
, a função Lucro, é de 2º grau. Logo trata-se de uma parábola. Para esta são conhecidas 2 fórmulasd que calculam seu "ponto de vértice" , isto é, calculam o seu valor máximo e para qual " x" este valor ocorre!
Seja a parábola
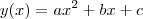
. O valor de x tal que ela se extremiza, isto é, atinge valor máximo ou mínimo é dado por
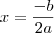
. Este valor é calculado por
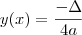
.
Para o seu problema identificamos,

,
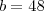
e
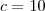
.
Portanto, o valor máximo desta função ( que será o Lucro máximo, pois y representa L, o lucro) é dado por
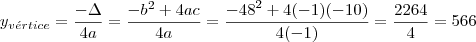
Assim, o lucro máximo será de 566 milhares de reais com a venda de 24 milhares de unidade2!
OBS:
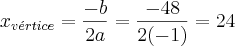
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Larice Mourao » Qui Mai 31, 2012 23:34
por Larice Mourao » Qui Mai 31, 2012 23:34
aaaa .. legal , entendi , estou muito grata !!
nunca mais esqueço que aquele ''L(x)'' significa a função lucro !!! hehe


-
Larice Mourao
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Mai 17, 2012 15:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação do 1º Grau - Como montar a equação
por macedo1967 » Sáb Out 07, 2017 12:53
- 1 Respostas
- 8036 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:17
Equações
-
- [Equação Modular] com equação de 2º grau
por paola-carneiro » Qui Abr 05, 2012 15:53
- 2 Respostas
- 3413 Exibições
- Última mensagem por paola-carneiro

Sex Abr 06, 2012 16:23
Funções
-
- [Função] isso é função do segundo grau?
por maulakalanata » Qua Mar 27, 2013 04:03
- 1 Respostas
- 2283 Exibições
- Última mensagem por timoteo

Qua Mar 27, 2013 10:51
Funções
-
- Equação do 1 Grau
por luanxd » Ter Jan 26, 2010 00:06
- 3 Respostas
- 5520 Exibições
- Última mensagem por Cleyson007

Qua Jan 27, 2010 20:40
Polinômios
-
- equação do 2º grau
por juniorthai » Seg Fev 08, 2010 12:05
- 2 Respostas
- 11755 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 06, 2010 20:48
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


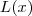 , a função Lucro, é de 2º grau. Logo trata-se de uma parábola. Para esta são conhecidas 2 fórmulasd que calculam seu "ponto de vértice" , isto é, calculam o seu valor máximo e para qual " x" este valor ocorre!
, a função Lucro, é de 2º grau. Logo trata-se de uma parábola. Para esta são conhecidas 2 fórmulasd que calculam seu "ponto de vértice" , isto é, calculam o seu valor máximo e para qual " x" este valor ocorre!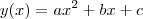 . O valor de x tal que ela se extremiza, isto é, atinge valor máximo ou mínimo é dado por
. O valor de x tal que ela se extremiza, isto é, atinge valor máximo ou mínimo é dado por 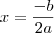 . Este valor é calculado por
. Este valor é calculado por 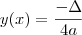 .
. ,
, 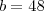 e
e 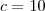 .
.