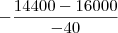por PeterHiggs » Sex Mai 25, 2012 22:24
por PeterHiggs » Sex Mai 25, 2012 22:24
Considere x,y
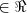
tais que 3x - y = 20. O menor valor de
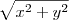
é:
a) 2
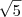
b) 2

c) 2

d) 4
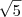
e) 4
 Resposta:
Resposta: Alternativa b)
* Bom, aqui está o que eu tentei fazer, mas obviamente não fechou com o resultado:
3x - y = 20
y = 3x - 20;
Substituindo na raiz:
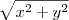

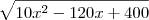
O valor sob a raiz sera o menor possível no vértice da parábola descrita pela função
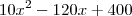
, já que o coeficiente de

é positivo (ou seja, concavidade pra cima, e valor mínimo).
yv =
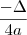
;
yv =
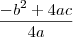
;
yv =
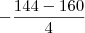
;
yv = 4;
Raiz de 4 é 2. Não fecha com nenhuma das alternativas. Alguém pode me indicar o caminho certo? Qual seria o menor valor assumido pelo expressão na raiz?
-
PeterHiggs
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Mai 25, 2012 18:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por PeterHiggs » Sáb Mai 26, 2012 16:09
por PeterHiggs » Sáb Mai 26, 2012 16:09
Ops, pessoal, foi mal. Cometi um ridículo equívoco com relação ao cálculo do yv na equação do 2° grau.
Simplifiquei a equação
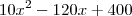
para
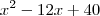
, e daí calculei o yv. Não sei porque fiz isso...
Me desculpem pela distração!
 Resolução correta:
Resolução correta:3x - y = 20
y = 3x - 20;
Substituindo na raiz:
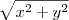

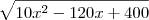
O valor sob a raiz sera o menor possível no vértice da parábola descrita pela função
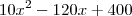
, já que o coeficiente de

é positivo (ou seja, concavidade pra cima, e valor mínimo).
yv =
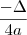
;
yv =
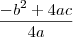
;
yv = 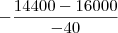 yv = 40;
yv = 40;Raiz de 40 é 2

.
Alternativa b)
-
PeterHiggs
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Mai 25, 2012 18:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Qual é o menor e o maior valor de x na expressão
por andersontricordiano » Seg Out 03, 2011 16:56
- 1 Respostas
- 3942 Exibições
- Última mensagem por MarceloFantini

Seg Out 03, 2011 21:10
Trigonometria
-
- menor valor de x
por stuart clark » Sáb Mai 28, 2011 00:41
- 0 Respostas
- 1797 Exibições
- Última mensagem por stuart clark

Sáb Mai 28, 2011 00:41
Trigonometria
-
- Qual deverá ser menor valor da força F
 por andersontricordiano » Qui Dez 15, 2011 11:44
por andersontricordiano » Qui Dez 15, 2011 11:44
- 5 Respostas
- 4607 Exibições
- Última mensagem por Fabricio dalla

Sex Dez 23, 2011 15:57
Mecânica
-
- [Geometria] O menor valor possível para soma.
 por my2009 » Ter Fev 09, 2016 10:59
por my2009 » Ter Fev 09, 2016 10:59
- 1 Respostas
- 4577 Exibições
- Última mensagem por Baltuilhe

Sáb Fev 20, 2016 19:27
Geometria
-
- Isolar uma variável numa equação de grau 3
por KleinIll » Dom Abr 24, 2016 16:37
- 0 Respostas
- 7160 Exibições
- Última mensagem por KleinIll

Dom Abr 24, 2016 16:37
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
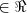 tais que 3x - y = 20. O menor valor de
tais que 3x - y = 20. O menor valor de 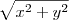 é:
é: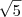


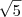

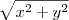

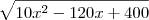
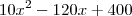 , já que o coeficiente de
, já que o coeficiente de  é positivo (ou seja, concavidade pra cima, e valor mínimo).
é positivo (ou seja, concavidade pra cima, e valor mínimo).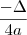 ;
;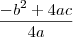 ;
;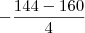 ;
;

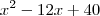 , e daí calculei o yv. Não sei porque fiz isso...
, e daí calculei o yv. Não sei porque fiz isso...