O problema e feito a volta de uma ponte em arco que faz uma parabola de diametro de 200, altura ou h=80 dois pontos A e B com altura de 50
este e o enunciado : Considerando que o arco é parte de uma parábola, escolhe um referencial e, relativamente a esse referencial, determina:
1. a equação da parábola;
2. a distância entre os pilares A e B
eu sei que y=a(x-h)^2+k
eu faltei a imensas aulas e nao faço ideia como descobrir "a" , por isto quero dizer que nao sei descobrir os pontos x e y da equaçao, ja me disseram que e um ponto ocalhas mas isso deixa a questao como e que eu descubro o y desse ponto.
a distancias entre os pilares nao faço mesmo ideia nenhuma como fazer
Qualquer ajuda era apreciada, obrigado.


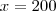 e a outra é
e a outra é  . Assim sabemos que o máximo da parabora é
. Assim sabemos que o máximo da parabora é 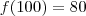 .
.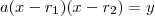 . Então:
. Então: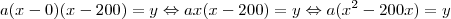
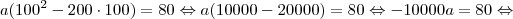
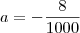
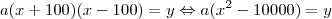
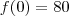 .
.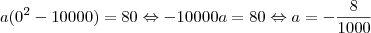
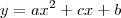 .
.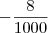 . O valor de
. O valor de 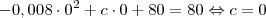
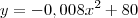
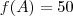 . Então:
. Então:
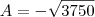 e
e 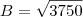 . Logo a distancia entre
. Logo a distancia entre 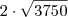

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.