 por Thulio_Parazi » Qui Mai 03, 2012 14:06
por Thulio_Parazi » Qui Mai 03, 2012 14:06
QUESTÃO 19
A inversa da função f : R ? R+ com f(x) = x² é a função g : R+ ? R
com g(x) = ?x,
PORQUE
a função f : X ? Y é a inversa de g : Y ? X se g o f(x) = x para todo
x ? X e f o g(y) = y para todo y ? Y.
Considerando o esquema proposição-razão acima, pode-se inferir
que
a) as duas são falsas.
b) a primeira é falsa e a segunda é verdadeira.
c) a primeira é verdadeira e a segunda é falsa.
d) as duas são verdadeiras e a segunda justifica a primeira.
e) as duas são verdadeiras e a segunda não justifica a primeira.
Como faço para resolver esse exercício ? Não sube nem por onde começar a resolver.
-
Thulio_Parazi
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Qui Abr 05, 2012 11:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Dom Mai 06, 2012 00:44
por MarceloFantini » Dom Mai 06, 2012 00:44
Primeiro é necessário conhecer a definição de função inversa, que é idêntica ao que a proposição diz. Portanto, ela é verdadeira. Agora você precisa entender como ela se aplica ao caso particular que ele cita, que é falso. Note que para que
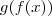
isto pode falhar. Tome
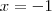
. Então
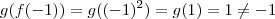
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- cefet-mg
por Thulio_Parazi » Ter Abr 10, 2012 10:06
- 2 Respostas
- 2432 Exibições
- Última mensagem por Thulio_Parazi

Seg Abr 16, 2012 11:50
Matrizes e Determinantes
-
- CEFET
por Thulio_Parazi » Qui Abr 19, 2012 11:30
- 3 Respostas
- 1975 Exibições
- Última mensagem por fraol

Qui Abr 19, 2012 23:38
Geometria Analítica
-
- cefet-mg 2012
por Thulio_Parazi » Ter Abr 10, 2012 09:55
- 1 Respostas
- 1607 Exibições
- Última mensagem por MarceloFantini

Ter Abr 10, 2012 21:12
Trigonometria
-
- cefet-mg 2012 log
por Thulio_Parazi » Ter Abr 10, 2012 14:37
- 5 Respostas
- 3776 Exibições
- Última mensagem por Thulio_Parazi

Qui Abr 12, 2012 09:26
Logaritmos
-
- [cefet mg matematica]
por tayna01 » Ter Abr 08, 2014 11:15
- 2 Respostas
- 2693 Exibições
- Última mensagem por tayna01

Qua Abr 09, 2014 13:28
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


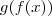 isto pode falhar. Tome
isto pode falhar. Tome 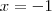 . Então
. Então 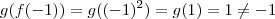 .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.