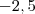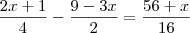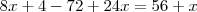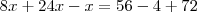por Andrewo » Qui Fev 16, 2012 09:28
por Andrewo » Qui Fev 16, 2012 09:28
Bom, fiz uma equação do 1º grau e o resultado foi uma fração, na hora de trocar o x por essa fração pra conferir se estava errado eu fiquei confuso na hora de resolver.
A equação é :
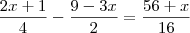
O resultado ficou em
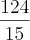
Mas agora pra conferir é que me confundiu
=
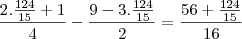
Como eu posso resolver isso?
E uma outra duvidazinha que não é fração : o que significa esse símbolo : |
Vi uma professora fazer
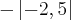
=
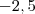
Vlwww


-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Ter Fev 21, 2012 16:30
por DanielFerreira » Ter Fev 21, 2012 16:30
Andrewo escreveu:Bom, fiz uma equação do 1º grau e o resultado foi uma fração, na hora de trocar o x por essa fração pra conferir se estava errado eu fiquei confuso na hora de resolver.
A equação é :
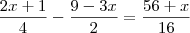
O resultado ficou em
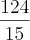
Mas agora pra conferir é que me confundiu
=
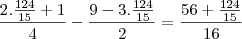
Como eu posso resolver isso?
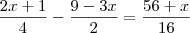
MMC(2, 4, 16) = 16

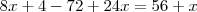
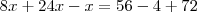

 Andrewo
Andrewo,
o que acha de postar sua solução, assim veremos onde está errando.
E uma outra duvidazinha que não é fração : o que significa esse símbolo : |
Vi uma professora fazer - |- 2,5| = - 2,5
É módulo!!
Ex.:
|- 1| = 1
|1| = 1
|- x| = x
No seu exemplo...
- |- 2,5| = ?
Agora, já sabe que: |- 2,5| = 2,5
então,
- |- 2,5|=
- (2,5) =
- 2,5
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida em frações algébricas
por LuizCarlos » Dom Abr 22, 2012 10:04
- 7 Respostas
- 3253 Exibições
- Última mensagem por DanielFerreira

Qui Abr 26, 2012 20:14
Álgebra Elementar
-
- Dúvida multiplicação de frações
por gutoponto7 » Qua Ago 15, 2012 10:30
- 1 Respostas
- 1508 Exibições
- Última mensagem por e8group

Qua Ago 15, 2012 12:21
Polinômios
-
- FRAÇÕES COM ARRANJOS - DÚVIDA EM EXERCÍCIO
por amateurfeet » Dom Mar 11, 2012 16:20
- 1 Respostas
- 2212 Exibições
- Última mensagem por LuizAquino

Seg Mar 12, 2012 12:57
Estatística
-
- [Frações] Regra de frações
por raymondtfr » Dom Nov 02, 2014 16:49
- 4 Respostas
- 3325 Exibições
- Última mensagem por Russman

Dom Nov 02, 2014 23:57
Aritmética
-
- FRAÇÕES
por csantos » Sex Ago 29, 2008 16:33
- 1 Respostas
- 3264 Exibições
- Última mensagem por admin

Sex Ago 29, 2008 16:47
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
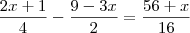
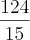
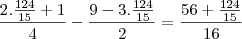
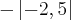 =
= 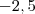



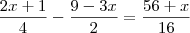
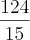
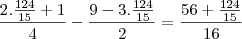
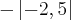 =
=