 por priscila1992 » Dom Fev 12, 2012 00:10
por priscila1992 » Dom Fev 12, 2012 00:10
Galerinha inteligentee, eu queriia tirar uma duvida:
estava estudando e no livro há uma questão assim
Elimine o módulo:
1. |-a| , se a > 0 a resposta é a
2. |-a| a resposta é -a, se a>=0 e a, se a < 0
eu não estou conseguindo entender as duas respostas diferentes. se puderem me explicar.
-
priscila1992
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Fev 12, 2012 00:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por fraol » Dom Fev 12, 2012 00:37
por fraol » Dom Fev 12, 2012 00:37
Módulo por definição, sempre, é um número positivo (ou nulo).
1. |-a| , se a > 0 a resposta é a
Ok. Se
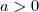
então
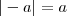
é um número positivo.
2. |-a| a resposta é -a, se a>=0 e a, se a < 0
Separando o que está escrito pode-se analisar da seguinte forma:
Errado: Se
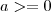
então
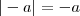
é um número negativo e contradiz a definição.
Errado: Se
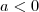
então
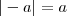
é um número negativo e contradiz a definição.
Deve haver um erro de digitação no livro.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- estou com duvida (inequaçoes com modulo)
por Fabricio dalla » Qui Mar 17, 2011 15:11
- 1 Respostas
- 1512 Exibições
- Última mensagem por LuizAquino

Qui Mar 17, 2011 15:58
Funções
-
- Duvida na aplicação de Modulo no vetor
por PatyMCastro » Qua Abr 20, 2011 14:47
- 6 Respostas
- 3543 Exibições
- Última mensagem por PatyMCastro

Qua Abr 27, 2011 00:34
Geometria Analítica
-
- Módulo
por Rodrigo Tomaz » Sex Fev 19, 2010 11:36
- 4 Respostas
- 3030 Exibições
- Última mensagem por MarceloFantini

Sex Mar 05, 2010 16:09
Funções
-
- Modulo
por Sandy26 » Ter Abr 27, 2010 14:46
- 5 Respostas
- 3012 Exibições
- Última mensagem por MarceloFantini

Qui Abr 29, 2010 17:57
Álgebra Elementar
-
- Módulo
por Bebel » Dom Ago 08, 2010 00:24
- 0 Respostas
- 1381 Exibições
- Última mensagem por Bebel

Dom Ago 08, 2010 00:24
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


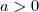 então
então 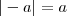 é um número positivo.
é um número positivo.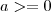 então
então 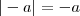 é um número negativo e contradiz a definição.
é um número negativo e contradiz a definição.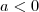 então
então 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.