Tenho dúvidas de como construir esta representação, não sei nem por onde começar... Agradeço pelo ajuda.
Utilizando régua e compasso, localize na reta real o número x= (3+?13)/2



 e altura 1, se aplicar pitágoras conseguirá o valor da hipotenusa que é
e altura 1, se aplicar pitágoras conseguirá o valor da hipotenusa que é ![\frac{\sqrt[]{13}}{2} \frac{\sqrt[]{13}}{2}](/latexrender/pictures/eb6b16103be7ad1a43eff2f521e0935e.png)
![\frac{\sqrt[]{13}}{2} \frac{\sqrt[]{13}}{2}](/latexrender/pictures/eb6b16103be7ad1a43eff2f521e0935e.png) e centro em
e centro em  tente terminar, falta só um pouco
tente terminar, falta só um pouco
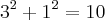 e não 13. E o ponto médio sobre a hipotenusa (diagonal do retângulo) é quem definirá o segmento de medida
e não 13. E o ponto médio sobre a hipotenusa (diagonal do retângulo) é quem definirá o segmento de medida ![\frac{\sqrt[2]{13}}{2} \frac{\sqrt[2]{13}}{2}](/latexrender/pictures/24acebc042aa7f454e2fd67a23a7d62d.png)

 e altura 1, porque
e altura 1, porque  , teremos:
, teremos: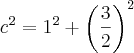

![\frac{\sqrt[]{13}}{2} \frac{\sqrt[]{13}}{2}](/latexrender/pictures/eb6b16103be7ad1a43eff2f521e0935e.png)


Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes