a) -5 b) -4 c) -8 d) -2 e) -6 resp: a) -5
Eu comecei assim:
f(x) = a(x - 1)(x - 9)
f(x) = a(x² -10x +9)
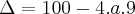
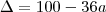
yv=-(100 -36a)/4a ?
Eu não entendi como resolvo esse "a". Agradeço se alguem puder ajudar.

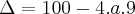
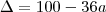

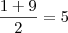
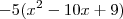
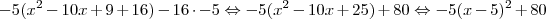


Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

