Dado
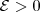 arbitrário, determine
arbitrário, determine 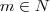 * tal que
* tal que  para todo
para todo 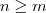 , onde
, onde 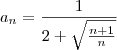 e
e 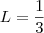
Eu fiz dessa maneira:
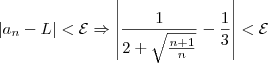
Mas,
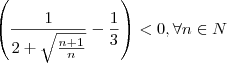 * (Isso é fácil provar, mas eu omiti para encurtar). Portanto,
* (Isso é fácil provar, mas eu omiti para encurtar). Portanto, 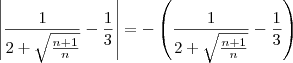
Voltando à inequação:
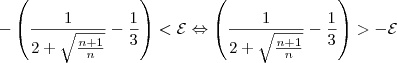
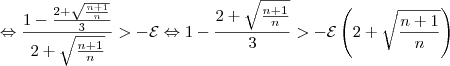
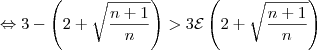
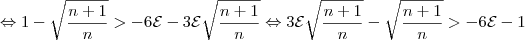
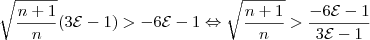
Agora, é preciso elevar ambos lados ao quadrado. No entanto, o membro à direita é negativo para alguns valores de
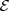 . Resolvendo a inequação
. Resolvendo a inequação 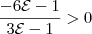 , encontra-se
, encontra-se 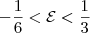 .
.Elevando-se ambos os lados ao quadrado, segue que:
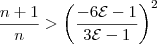
Com mais algumas manipulações algébricas, (omitidas para não deixar o post ainda mais extenso), chega-se em:
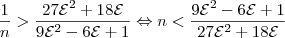
No gabarito, está
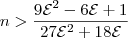
Realmente, não faz sentido chegar a um resultado em que n deve ser menor do que alguma coisa, pois o enunciado pede um
 tal que
tal que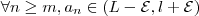
Gostaria que alguém apontasse onde eu errei.


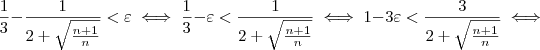
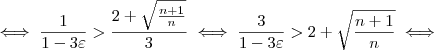
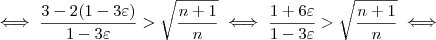
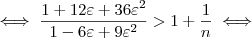
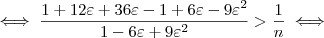
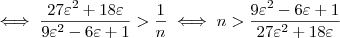




 , avisa que eu resolvo.
, avisa que eu resolvo.

