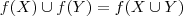por Aliocha Karamazov » Sáb Jul 09, 2011 02:02
por Aliocha Karamazov » Sáb Jul 09, 2011 02:02
Galera, tenho um exercício de demonstrar as propriedade da imagem de uma função. Sempre que posto no fórum, mostro como tentei fazer o exercício. Dessa vez, o problema é que não sei como demonstrar nesse caso específico. Gostaria de uma ajuda no primeiro exercício, aí eu faço os outros...
Só para deixar claro,
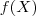
denota a imagem do conjunto X através da função f. X é um subconjunto do domínio. O exercício é esse:
Prove que
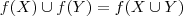
Agradeço a quem puder ajudar.
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por Guill » Dom Jul 10, 2011 09:33
por Guill » Dom Jul 10, 2011 09:33
Sejam f(x) e f(y) duas imagens das respectívas funções x e y. Sendo assim:
f(x)?f(y) representa a união das imagens dos conjuntos x e y.
Sabe-se que a imagem de um conjunto é obtida pelos valores de seu domínio. Como x e y são os domínios das funções f(x) e f(y), f(x)?f(y) é o agrupamento das imagens. Sabemos que as imagens f(x) e f(y) são obtidas a partir de x e y. Logo, se reunirmos os termos que foram usados para encontrar as imagens f(x) e f(y) e jogarmos na função, teremos os mesmos valores. Com isso:
f(x?y) = f(x)?f(y)
Poderia ter feito assim:
Seja x e y, conjuntos tais que:
x = {a;b;c;d;e...}
y = {f;g;h;i;j...}
As imagens f(x) e f(y) são:
f(x) = f(a) ; f(b) ; f(c) ; f(d) ; f(e)...
f(y) = f(f) ; f(g) ; f(h) ; f(i) ; f(j)...
Podemos definir assim:
x?y = {a;b;c;d;e...f;g;h;i;j...}
A união das imagens é:
f(x)?f(y) = f(a) ; f(b) ; f(c) ; f(d) ; f(e)...f(f) ; f(g) ; f(h) ; f(i) ; f(j)...
Sabe-se que:
f(x?y) = f(a) ; f(b) ; f(c) ; f(d) ; f(e)...f(f) ; f(g) ; f(h) ; f(i) ; f(j)... pois x?y = {a;b;c;d;e...f;g;h;i;j...}. Sendo assim, podemos determinar que:
f(x?y) = f(x)?f(y)
-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Prove usando a Propriedade Arquimediana...] Propriedade Arq
por alessandro » Seg Abr 16, 2012 19:10
- 1 Respostas
- 1524 Exibições
- Última mensagem por alessandro

Seg Abr 16, 2012 19:12
Sequências
-
- Demonstre!
por Abelardo » Dom Abr 10, 2011 12:01
- 3 Respostas
- 1584 Exibições
- Última mensagem por Abelardo

Dom Abr 10, 2011 17:52
Álgebra Elementar
-
- Racionais: propriedade
por Victor Gabriel » Dom Mai 12, 2013 15:58
- 0 Respostas
- 1310 Exibições
- Última mensagem por Victor Gabriel

Dom Mai 12, 2013 15:58
Álgebra Elementar
-
- [Radiciação Propriedade 6]
 por soccol » Sex Set 26, 2014 18:34
por soccol » Sex Set 26, 2014 18:34
- 0 Respostas
- 889 Exibições
- Última mensagem por soccol

Sex Set 26, 2014 18:34
Álgebra Elementar
-
- Propriedade logaritmo - dúvida
por Fernanda Lauton » Sáb Jun 26, 2010 18:27
- 2 Respostas
- 1753 Exibições
- Última mensagem por Fernanda Lauton

Seg Jun 28, 2010 10:12
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
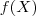 denota a imagem do conjunto X através da função f. X é um subconjunto do domínio. O exercício é esse:
denota a imagem do conjunto X através da função f. X é um subconjunto do domínio. O exercício é esse: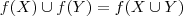

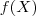 denota a imagem do conjunto X através da função f. X é um subconjunto do domínio. O exercício é esse:
denota a imagem do conjunto X através da função f. X é um subconjunto do domínio. O exercício é esse: