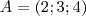 e
e 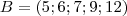 , qual o conjunto Im da função de
, qual o conjunto Im da função de 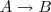 tal que
tal que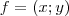

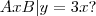
Tipo, eu tentei resolver e cheguei a essa conclusão,
 é a formula para que o conjunto
é a formula para que o conjunto  , seja multiplicado por
, seja multiplicado por  e o conjunto Im seja feito correto?
e o conjunto Im seja feito correto?No gabarito diz o contrario! Não entendi.

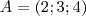 e
e 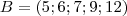 , qual o conjunto Im da função de
, qual o conjunto Im da função de 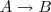 tal que
tal que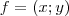

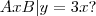
 é a formula para que o conjunto
é a formula para que o conjunto  , seja multiplicado por
, seja multiplicado por  e o conjunto Im seja feito correto?
e o conjunto Im seja feito correto?

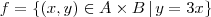
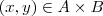 significa que você pegou um par de elementos x e y onde
significa que você pegou um par de elementos x e y onde 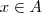 e
e  .
.

 , significa que, ela só será aplicada no subconjunto de "
, significa que, ela só será aplicada no subconjunto de " " ? que pode ser chamado de relação correto?
" ? que pode ser chamado de relação correto?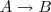 tal que
tal que 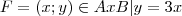 " Ele está pedindo
" Ele está pedindo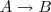 ? ... Significa intercessão de
? ... Significa intercessão de  EM
EM  ?
? 

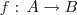 quer dizer que a função está definida em A e quando aplicamos a regra os resultados são elementos de B. Computar uma função quer dizer calculá-la. O que você pensa ser aplicada no conjunto B? A forma de pensar é a seguinte: você vai pegar os elementos de A e aplicar a regra, ou seja, vai encontrar quanto é a função aplicada em cada elemento. O conjunto formado por esses elementos resultantes é o que chamamos de conjunto imagem da função, que é um subconjunto de B, ou seja, são pontos de B também.
quer dizer que a função está definida em A e quando aplicamos a regra os resultados são elementos de B. Computar uma função quer dizer calculá-la. O que você pensa ser aplicada no conjunto B? A forma de pensar é a seguinte: você vai pegar os elementos de A e aplicar a regra, ou seja, vai encontrar quanto é a função aplicada em cada elemento. O conjunto formado por esses elementos resultantes é o que chamamos de conjunto imagem da função, que é um subconjunto de B, ou seja, são pontos de B também. , você tem que perceber que y é um elemento de B e x é um elemento de A. Você já tem os valores de x, que são os elementos de A, e você quer descobrir quais são os correspondentes em B, ou seja, aplique a regra e você encontrará os elementos.
, você tem que perceber que y é um elemento de B e x é um elemento de A. Você já tem os valores de x, que são os elementos de A, e você quer descobrir quais são os correspondentes em B, ou seja, aplique a regra e você encontrará os elementos.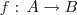 : uma forma de interpretar é que a função f leva elementos de A em elementos de B. Essa interpretação é a que deve guardar.
: uma forma de interpretar é que a função f leva elementos de A em elementos de B. Essa interpretação é a que deve guardar.

Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes

 .
.



