a) Qual o tamanho da população após 15 horas?
b) Qual o tamanho da população após t horas?( determine o número de bactérias em função de t)
c) Qual o tamanho da população após 20 horas?
d) Encontre a função inversa a função determinada na letra c) e explique seu significado
e) Quando a população atingirá 50.000 bactérias?
a)
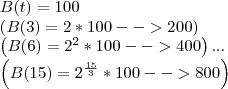
b)
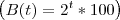
c)
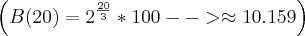
d)
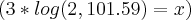
e)
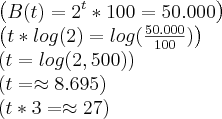
MInha dúvida maior é quanto a inversa.
Se alguém puder dar uma analisada, eu agradeço!
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)