Olá Boa Tarde! Estou tentando de várias formas resolver esse seguinte problema q não estou conseguindo, eu tenho muita duvida com a matematica, me ajudem por favor!!!
Pedro e Paulo têm certo número de laranjas. Se Paulo desse a Pedro 12 laranjas, cada um teria o mesmo numero. Pelo contrário, se Pedro desse os 3/5 das suas a Paulo o numero de laranjas de Paulo seria aumentado de seus 3/8. Qual o total de laranjas?
tentei fazer da seguinte forma:
nº de laranja - x
laranja dada à pedro: 12 laranjas
// dada à paulo: 3/5
???? Daí não consegui fazer mas nada, ou seja, não consegui nem montar o problema!


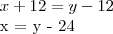
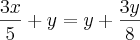

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)