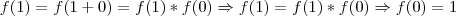por Abelardo » Sáb Abr 09, 2011 19:15
por Abelardo » Sáb Abr 09, 2011 19:15
Sabendo-se que
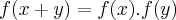
para qualquer valor real x e qualquer valor real y, é valido afirmar-se que :
a)f(0)=1
b)f(1)=1
c)f(0)=0
d)f(1)=0
e)f(-1)=f(1)
Como proceder a ''magia'' da questão?
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Sáb Abr 09, 2011 20:51
por Molina » Sáb Abr 09, 2011 20:51
Abelardo, perceba que:
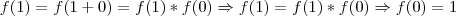

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Abelardo » Sáb Abr 09, 2011 21:26
por Abelardo » Sáb Abr 09, 2011 21:26
Molina, deparo-me com várias questões desse tipo. Existe alguma técnica para resolução dela, ou só com prática e muita observação para encontrar a solução?
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Fabricio dalla » Sáb Abr 09, 2011 22:48
por Fabricio dalla » Sáb Abr 09, 2011 22:48
Molina nesse tipo de questão x e y so admitirão valores inteiros ?
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Sáb Abr 09, 2011 23:20
por Molina » Sáb Abr 09, 2011 23:20
Boa noite.
Abelardo escreveu:Molina, deparo-me com várias questões desse tipo. Existe alguma técnica para resolução dela, ou só com prática e muita observação para encontrar a solução?
Não há tecnica especial. É mais em observar as ferramentas que você tem e praticar um algebrismo que se adquire com a prática. As vezes este 'estalo' inicial é difícil de perceber mesmo.
Fabricio dalla escreveu:Molina nesse tipo de questão x e y so admitirão valores inteiros ?
O enunciado diz que pode ser qualquer valor real. E particularmente não vejo nenhum impedimento nisso, Fabricio. Você observou alguma falha?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Abelardo » Sáb Abr 09, 2011 23:32
por Abelardo » Sáb Abr 09, 2011 23:32
A resposta está certíssima..
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Fabricio dalla » Sáb Abr 09, 2011 23:45
por Fabricio dalla » Sáb Abr 09, 2011 23:45
não, observei não, ta certo eu q tava pensando besteira
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ajuda
por Daiane kelly » Seg Mar 24, 2008 22:38
- 4 Respostas
- 6209 Exibições
- Última mensagem por Cleyson007

Ter Mai 12, 2009 17:43
Matrizes e Determinantes
-
- Ajuda
por Umbus » Sáb Out 18, 2008 14:12
- 2 Respostas
- 3552 Exibições
- Última mensagem por lopes

Sáb Jun 20, 2009 15:51
Álgebra Linear
-
- Ajuda.
por VanessaFontela » Qui Dez 04, 2008 10:32
- 0 Respostas
- 2814 Exibições
- Última mensagem por VanessaFontela

Qui Dez 04, 2008 10:32
Matemática Financeira
-
- Ajuda!!!
por GABRIELA » Seg Set 21, 2009 17:28
- 1 Respostas
- 2185 Exibições
- Última mensagem por Molina

Seg Set 21, 2009 19:56
Sistemas de Equações
-
- Ajuda!!!!!!
por GABRIELA » Ter Set 22, 2009 16:35
- 6 Respostas
- 4186 Exibições
- Última mensagem por GABRIELA

Qui Set 24, 2009 16:29
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
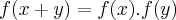 para qualquer valor real x e qualquer valor real y, é valido afirmar-se que :
para qualquer valor real x e qualquer valor real y, é valido afirmar-se que :
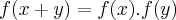 para qualquer valor real x e qualquer valor real y, é valido afirmar-se que :
para qualquer valor real x e qualquer valor real y, é valido afirmar-se que :