Esse é um conteúdo que deve (ou deveria) ser visto ao ensinarmos a resolução de equações do 2º grau no ensino fundamental.
A ideia básica é determinar x e y positivos tais que

. Desse modo, temos que

.
Note que determinar esse x e y consiste em resolver o sistema:

Mas, esse sistema é equivalente a:

Desse modo, queremos determinar dois números cuja a soma seja
a e o produto seja
b/4. Ou seja, queremos as soluções da equação:

Essa equação só possui soluções reais se

. Nesse caso, as soluções serão:

e

.
Portanto, teremos que:

Agora, chamando

, chegamos na relação:

Por fim, note que essa estratégia só é interessante se

for racional. Se isso fosse irracional, teríamos que

para algum
d. Daí a simplificação não seria interessante, pois ficaríamos com:

Vale destacar que no caso particular da equação

, o caminho mais simples é mesmo analisar a soma e o produto das raízes.
Entretanto, imagine que o exercício fosse resolver a equação

. Duas raízes para essa equação são

e

. Note que seria difícil ter chegado nessa solução usando a estratégia de analisar a soma e o produto das raízes. Entretanto, usando a estratégia acima podemos chegar nesse resultado.
 , enquanto calculava o delta cheguei nisso:
, enquanto calculava o delta cheguei nisso: 

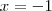 e
e 


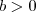

 seja racional,temos:
seja racional,temos:
 não for racional.
não for racional.









 e multiplicados
e multiplicados  ? Fica um tanto quanto nítido. Não sei ele já ensinou isso, portanto talvez desconsidere. O caso é que eu acho que esse método pelo tal "radical duplo" é usar um canhão para matar uma formiga. Acho específico demais (pessoalmente nunca vi isso em nenhuma prova, vestibular, livro de ensino médio ou matéria da universidade) para ser usado num único problema. Deve existir um outro jeito de visualizar, possivelmente sem ser o meu ou do radical, de forma mais natural e sem uso de tal artifício.
? Fica um tanto quanto nítido. Não sei ele já ensinou isso, portanto talvez desconsidere. O caso é que eu acho que esse método pelo tal "radical duplo" é usar um canhão para matar uma formiga. Acho específico demais (pessoalmente nunca vi isso em nenhuma prova, vestibular, livro de ensino médio ou matéria da universidade) para ser usado num único problema. Deve existir um outro jeito de visualizar, possivelmente sem ser o meu ou do radical, de forma mais natural e sem uso de tal artifício.

 . Desse modo, temos que
. Desse modo, temos que  .
.


 . Nesse caso, as soluções serão:
. Nesse caso, as soluções serão:  e
e  .
.
 , chegamos na relação:
, chegamos na relação:
 for racional. Se isso fosse irracional, teríamos que
for racional. Se isso fosse irracional, teríamos que  para algum
para algum 
 , o caminho mais simples é mesmo analisar a soma e o produto das raízes.
, o caminho mais simples é mesmo analisar a soma e o produto das raízes. . Duas raízes para essa equação são
. Duas raízes para essa equação são  e
e  . Note que seria difícil ter chegado nessa solução usando a estratégia de analisar a soma e o produto das raízes. Entretanto, usando a estratégia acima podemos chegar nesse resultado.
. Note que seria difícil ter chegado nessa solução usando a estratégia de analisar a soma e o produto das raízes. Entretanto, usando a estratégia acima podemos chegar nesse resultado. e
e  .
. para transformá-lo em
para transformá-lo em  .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)