 por 380625 » Seg Fev 28, 2011 12:54
por 380625 » Seg Fev 28, 2011 12:54
Bom dia estou com muita dificuldades para resolver equações desse tipo:
Se 0<x<pi, as raizes da equação cos^2x - sen ^2( pi - x)=1/2 são:
Obs: o x esta no intervalo o menor igual a x e menor igual a pi.
-
380625
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Sex Fev 18, 2011 17:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Seg Fev 28, 2011 18:05
por LuizAquino » Seg Fev 28, 2011 18:05
380625 escreveu:Se
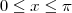
, as raízes da equação
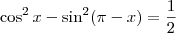
são:
Sabemos que
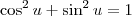
, para qualquer ângulo
u. Portanto, a equação é equivalente a:
![\cos^2x - [1 - \cos ^2(\pi - x)]=\frac{1}{2} \cos^2x - [1 - \cos ^2(\pi - x)]=\frac{1}{2}](/latexrender/pictures/79fd8ff8a24b7e161d25a54d5c4bfc88.png)
Lembrando-se que
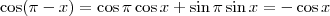
, temos que:
![\cos^2x - [1 - (-\cos x)^2]=\frac{1}{2} \cos^2x - [1 - (-\cos x)^2]=\frac{1}{2}](/latexrender/pictures/6efea19b1c0b8ca487a23805103b4b27.png)
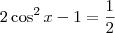
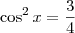
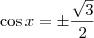
O ângulo do primeiro quadrante que tem cosseno igual a
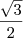
é
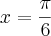
. Já o ângulo do segundo quadrante que tem cosseno igual a
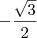
é
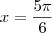
. Portanto, as raízes são
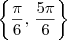
380625 escreveu:estou com muita dificuldades para resolver equações desse tipo
Muito provavelmente essa dificuldade deve-se ao fato de você não conhecer as identidades trigonométricas. Não tem jeito: você tem que estudá-las antes de fazer equações assim.
380625 escreveu:Obs: o x esta no intervalo o menor igual a x e menor igual a pi.
Por favor, faça uso do recurso LaTeX disponível aqui no fórum para digitar os símbolos adequados. Se ainda não estiver bem treinado, você pode usar o botão "Editor de Fórmulas", disponível na edição de suas mensagens.

- botao-editor-de-formulas.png (2.82 KiB) Exibido 674 vezes
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funções reais. como resolver estas funções...
por LEANDRO HENRIQUE » Ter Mar 04, 2014 18:43
- 0 Respostas
- 3272 Exibições
- Última mensagem por LEANDRO HENRIQUE

Ter Mar 04, 2014 18:43
Funções
-
- [Funções] Domínio e a imagem de funções
 por concurseironf » Qui Ago 21, 2014 12:24
por concurseironf » Qui Ago 21, 2014 12:24
- 1 Respostas
- 4002 Exibições
- Última mensagem por Pessoa Estranha

Sex Ago 22, 2014 20:11
Funções
-
- [Funções] questões de funções
por Zandrojr » Qua Ago 31, 2011 11:39
- 0 Respostas
- 2988 Exibições
- Última mensagem por Zandrojr

Qua Ago 31, 2011 11:39
Funções
-
- Funções
por Revelants » Dom Out 05, 2008 15:07
- 1 Respostas
- 3230 Exibições
- Última mensagem por Molina

Dom Out 05, 2008 15:53
Cálculo: Limites, Derivadas e Integrais
-
- Funçoes
por Luna » Seg Set 28, 2009 20:02
- 1 Respostas
- 2841 Exibições
- Última mensagem por Marcampucio

Seg Set 28, 2009 21:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



, as raízes da equação
são:
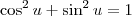 , para qualquer ângulo u. Portanto, a equação é equivalente a:
, para qualquer ângulo u. Portanto, a equação é equivalente a:![\cos^2x - [1 - \cos ^2(\pi - x)]=\frac{1}{2} \cos^2x - [1 - \cos ^2(\pi - x)]=\frac{1}{2}](/latexrender/pictures/79fd8ff8a24b7e161d25a54d5c4bfc88.png)
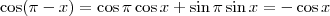 , temos que:
, temos que: ![\cos^2x - [1 - (-\cos x)^2]=\frac{1}{2} \cos^2x - [1 - (-\cos x)^2]=\frac{1}{2}](/latexrender/pictures/6efea19b1c0b8ca487a23805103b4b27.png)
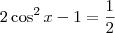
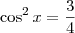
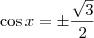
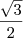 é
é 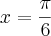 . Já o ângulo do segundo quadrante que tem cosseno igual a
. Já o ângulo do segundo quadrante que tem cosseno igual a 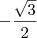 é
é 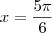 . Portanto, as raízes são
. Portanto, as raízes são 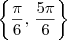

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
