Um fanático torcedor de um time de futebol decide revestir uma parede de 2,40m de altura por 9,60 de largura, que tem no fundo de seu quintal, com as três cores do time para o qual torce. Sabendo que todas as cerâmicas medem o,o5m por 0,20m já colocadas e que o torcedor possui peças suficientes nas cores preta e branca, mas que da cerâmica cinza ele só possui 30 peças, a quantidade mínima de cerâmicas na cor cinza que ele deverá comprar de modo a revestir toda a parede é igual a :
a) 95 peças
b) 670 peças
c) 770 peças
d) 1.500 peças
d) 2.304 peças
0BS: Eu não sei se se coloquei no lugar certo, sinceramente, não sei se isso é Trigonometria, eu aprendi isso o ano passado e não lembro mais, e esse ano eu não fiz nada parecido com esse exercício.
Muito Obrigada!!


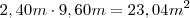 .
.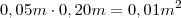 .
.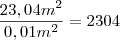 peças.
peças.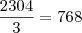 peças .
peças .
