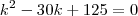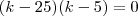por Rafael16 » Sáb Jul 07, 2012 13:47
por Rafael16 » Sáb Jul 07, 2012 13:47
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por DanielFerreira » Sáb Jul 07, 2012 16:27
por DanielFerreira » Sáb Jul 07, 2012 16:27
Rafael,
até onde fez está certo, no entanto, é mais complicado!
Mas há outro caminho, veja:
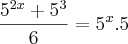
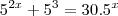
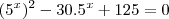
Considere

, então:
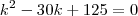
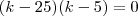
Portanto,
k = 5k = 25Agora poderá encontrar os valores de
x.
Espero ter ajudado!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação exponencial???
por azheng » Sáb Nov 21, 2009 19:47
- 0 Respostas
- 1625 Exibições
- Última mensagem por azheng

Sáb Nov 21, 2009 19:47
Álgebra Elementar
-
- Equação Exponencial
por Adriana Baldussi » Seg Nov 23, 2009 14:41
- 3 Respostas
- 2840 Exibições
- Última mensagem por Molina

Seg Nov 23, 2009 17:07
Álgebra Elementar
-
- Equação Exponencial
por LeonardoSantos » Ter Fev 16, 2010 14:11
- 1 Respostas
- 2829 Exibições
- Última mensagem por Douglasm

Ter Fev 16, 2010 15:46
Funções
-
- Equação exponencial
por cristina » Sex Jun 04, 2010 20:19
- 1 Respostas
- 2242 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 00:27
Sistemas de Equações
-
- Equação exponencial
por nan_henrique » Sáb Jul 10, 2010 13:00
- 1 Respostas
- 2193 Exibições
- Última mensagem por Douglasm

Sáb Jul 10, 2010 13:12
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
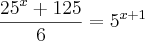
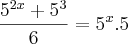
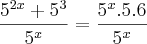
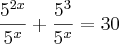
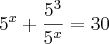
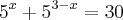


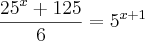
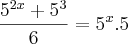
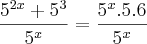
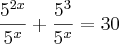
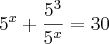
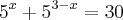


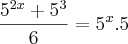
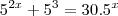
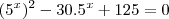
 , então:
, então: