 por LuizCarlos » Sáb Mai 05, 2012 00:14
por LuizCarlos » Sáb Mai 05, 2012 00:14
Olá amigos professores! estou aqui resolvendo uns exercícios, porém essa questão não estou conseguindo resolver!
![\sqrt[]{169{x}^{2}+104xy+16{y}^{2}} = \sqrt[]{{13}^{2}.{x}^{2}+{2}^{2}.13.2+{2}^{2}.{2}^{2}.{y}^{2}}=\sqrt[]{{13}^{2}.{x}^{2}}+\sqrt[]{{2}^{2}.26}+\sqrt[]{{2}^{2}.{2}^{2}.{y}^{2}}= 13.x + 2.\sqrt[]{26}+ 4.y \sqrt[]{169{x}^{2}+104xy+16{y}^{2}} = \sqrt[]{{13}^{2}.{x}^{2}+{2}^{2}.13.2+{2}^{2}.{2}^{2}.{y}^{2}}=\sqrt[]{{13}^{2}.{x}^{2}}+\sqrt[]{{2}^{2}.26}+\sqrt[]{{2}^{2}.{2}^{2}.{y}^{2}}= 13.x + 2.\sqrt[]{26}+ 4.y](/latexrender/pictures/ba686c39d12a5bcbc0ac284988628376.png)
Não estou conseguindo entender como resolver! tentei dessa forma! obrigado desde já.
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por MarceloFantini » Sáb Mai 05, 2012 00:38
por MarceloFantini » Sáb Mai 05, 2012 00:38
Luiz Carlos, isto é falso. Note que
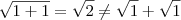
, por exemplo.
Para a resolução deste problema é necessário perceber um trinômio quadrado perfeito:
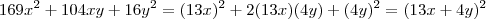
.
Colocando a raíz quadrada, temos
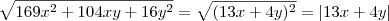
onde
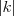
representa o módulo do valor. Provavelmente é aceitável que você dê a resposta como

caso ainda não tenha aprendido isto.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizCarlos » Sáb Mai 05, 2012 10:25
por LuizCarlos » Sáb Mai 05, 2012 10:25
MarceloFantini escreveu:Luiz Carlos, isto é falso. Note que
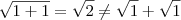
, por exemplo.
Para a resolução deste problema é necessário perceber um trinômio quadrado perfeito:
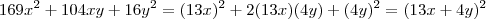
.
Colocando a raíz quadrada, temos
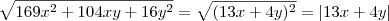
onde
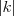
representa o módulo do valor. Provavelmente é aceitável que você dê a resposta como

caso ainda não tenha aprendido isto.
Obrigado MarceloFantine, agora conseguir perceber esse trinômio quadrado perfeito! gostaria de saber a respeito dessa questão de módulo que você citou!
como ficaria com essa resposta!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por MarceloFantini » Sáb Mai 05, 2012 14:00
por MarceloFantini » Sáb Mai 05, 2012 14:00
É que temos a definição que
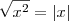
, portanto apenas apliquei a definição. O módulo garante que seja um número positivo e portanto que a raíz seja positiva.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Simplificação de raízes.
por Sobreira » Qui Mai 09, 2013 22:21
- 1 Respostas
- 1320 Exibições
- Última mensagem por brunnkpol

Qui Mai 09, 2013 23:49
Aritmética
-
- simplificação de raízes
por ezidia51 » Seg Mar 12, 2018 23:39
- 2 Respostas
- 2766 Exibições
- Última mensagem por ezidia51

Ter Mar 13, 2018 12:21
Aritmética
-
- [simplificação de expressoes] eliminar raizes
por bira19 » Qui Out 06, 2011 23:33
- 2 Respostas
- 2446 Exibições
- Última mensagem por bira19

Dom Out 09, 2011 17:47
Álgebra Elementar
-
- Simplificação - Ajuda Dúvidas em relação a simplificação
por wgf » Qui Mai 16, 2013 12:56
- 1 Respostas
- 2357 Exibições
- Última mensagem por DanielFerreira

Dom Mai 19, 2013 18:03
Equações
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8121 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{169{x}^{2}+104xy+16{y}^{2}} = \sqrt[]{{13}^{2}.{x}^{2}+{2}^{2}.13.2+{2}^{2}.{2}^{2}.{y}^{2}}=\sqrt[]{{13}^{2}.{x}^{2}}+\sqrt[]{{2}^{2}.26}+\sqrt[]{{2}^{2}.{2}^{2}.{y}^{2}}= 13.x + 2.\sqrt[]{26}+ 4.y \sqrt[]{169{x}^{2}+104xy+16{y}^{2}} = \sqrt[]{{13}^{2}.{x}^{2}+{2}^{2}.13.2+{2}^{2}.{2}^{2}.{y}^{2}}=\sqrt[]{{13}^{2}.{x}^{2}}+\sqrt[]{{2}^{2}.26}+\sqrt[]{{2}^{2}.{2}^{2}.{y}^{2}}= 13.x + 2.\sqrt[]{26}+ 4.y](/latexrender/pictures/ba686c39d12a5bcbc0ac284988628376.png)

![\sqrt[]{169{x}^{2}+104xy+16{y}^{2}} = \sqrt[]{{13}^{2}.{x}^{2}+{2}^{2}.13.2+{2}^{2}.{2}^{2}.{y}^{2}}=\sqrt[]{{13}^{2}.{x}^{2}}+\sqrt[]{{2}^{2}.26}+\sqrt[]{{2}^{2}.{2}^{2}.{y}^{2}}= 13.x + 2.\sqrt[]{26}+ 4.y \sqrt[]{169{x}^{2}+104xy+16{y}^{2}} = \sqrt[]{{13}^{2}.{x}^{2}+{2}^{2}.13.2+{2}^{2}.{2}^{2}.{y}^{2}}=\sqrt[]{{13}^{2}.{x}^{2}}+\sqrt[]{{2}^{2}.26}+\sqrt[]{{2}^{2}.{2}^{2}.{y}^{2}}= 13.x + 2.\sqrt[]{26}+ 4.y](/latexrender/pictures/ba686c39d12a5bcbc0ac284988628376.png)

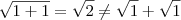 , por exemplo.
, por exemplo.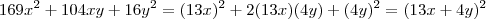 .
.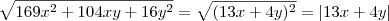
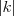 representa o módulo do valor. Provavelmente é aceitável que você dê a resposta como
representa o módulo do valor. Provavelmente é aceitável que você dê a resposta como  caso ainda não tenha aprendido isto.
caso ainda não tenha aprendido isto.

, por exemplo.
.
representa o módulo do valor. Provavelmente é aceitável que você dê a resposta como
caso ainda não tenha aprendido isto.

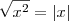 , portanto apenas apliquei a definição. O módulo garante que seja um número positivo e portanto que a raíz seja positiva.
, portanto apenas apliquei a definição. O módulo garante que seja um número positivo e portanto que a raíz seja positiva.
