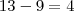por Mickdark » Dom Abr 08, 2012 20:00
por Mickdark » Dom Abr 08, 2012 20:00
Boa Noite!!
Gostaria de tirar uma dúvida, para tirar a raiz quadrada de 13 na mão, estou fazendo com alguns exemplos que eu vi na internet, mas o resultado decimal não é igual ao da calculadora!!! Alguem poderia me dizer onde estou errando!?
sqrt de 13 | 3 => gera 9, sobra 4
-9
4 00 => Aqui já começa o problema, se eu multiplicar utilizando a regra, eu baixo os dois zeros para uma casa decimal e quando multiplico gera 94 * 4 = 376 que iria para 3,4 (o qociente) , mas na calculadora o correto seria [3,6]0555..., só que 96*6 = 576 (que passa de 400).
-
Mickdark
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Abr 08, 2012 19:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por fraol » Qua Abr 11, 2012 21:47
por fraol » Qua Abr 11, 2012 21:47
Presumo que você esteja se referindo à seguinte fórmula, baseada na teoria das frações contínuas, que dá uma boa aproximação para raízes quadradas, tanto mais precisa quanto maior o número de frações agregadas.
Eis a fórmula:
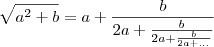
Nessa fórmula temos:

é o maior número inteiro que ao quadrado não supera o radicando.

é o resto obtido entre o radicando e o valor de
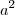
.
Vamos aplicar a fórmula ao caso da

mas com apenas duas frações.
Você já verificou os valores de

e

que são

e

respectivamente. Então:
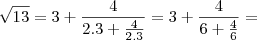
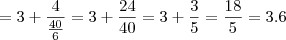
.
Assim se você usar mais frações, com um pouco mais de trabalho, obterá aproximações melhores.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Mickdark » Qui Abr 12, 2012 01:02
por Mickdark » Qui Abr 12, 2012 01:02
Pow cara, legal!!! Esse método eu não sabia, como desse jeito que eu passei no forum eu não consegui, eu acabei procurando por outro método, e acabei fazendo, mas eu queria saber realmente como faz a raiz quadrada pelo primeiro método que eu passei, eu me baseei neste vídeo:
http://www.youtube.com/watch?v=RXn25DQiqLIAcho que o que ele explica é diferente desse método das frações, mas de qualquer maneira, muito Obrigado, isso foi de grande ajuda também ^^.
-
Mickdark
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Abr 08, 2012 19:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por fraol » Qui Abr 12, 2012 07:45
por fraol » Qui Abr 12, 2012 07:45
Bom dia,
Seguindo o raciocínio para

, conforme explicado no vídeo:
(1) Maior número que ao quadrado não supera
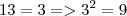
Então 3 é o primeiro algarismo da raiz.
(2)
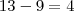
(3) Dobrar o número encontrado em (1)

(4) Como 6 é maior do que 4, acrescentamos um par de zeros ao 4que ficará igual a 400 ( assim teremos uma casa decimal de aproximação ).
(5) Devemos entrontrar um número que ao juntarmos ao 6 e multiplicado por esse mesmo número dê um valor menor ou igual a 400, isto é: 6 __ X __ = ____ <= 400.
(6) Tal número é o 6 pois: 66 x 6 = 396 <= 400 (resta 4). Então 6 também é algarismo da raiz, nesse caso 6 é o primeiro dígito decimal.
(7) Assim a raiz de 13 é igual à 3.6 com uma casa decimal.
Para obter mais casas decimais deve-se agregar 00 ao último resto e repetir o procedimento. Obs. Esse método é uma mecanização (forma prática) do cálculo das frações contínuas.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Mickdark » Qui Abr 12, 2012 09:56
por Mickdark » Qui Abr 12, 2012 09:56
haaaaaa, puts, eu entendi o que eu tava fazendo de errado, eu estava elevando ao quadrado ao invés de multiplicar por dois, por isso não estava conseguindo fazer!!! Fraol, muito obrigado pela ajuda, vc é joinha ^^
-
Mickdark
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Abr 08, 2012 19:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Raiz Cúbica e Raiz Quadrada] Muito difícil achar a solução.
por Leocondeuba » Sáb Mai 11, 2013 19:27
- 2 Respostas
- 7459 Exibições
- Última mensagem por Leocondeuba

Sáb Mai 11, 2013 20:42
Aritmética
-
- Raiz quadrada
por j1a4l0 » Qui Abr 22, 2010 18:05
- 5 Respostas
- 5995 Exibições
- Última mensagem por Neperiano

Sex Abr 23, 2010 09:35
Funções
-
- raiz quadrada
por jose henrique » Seg Ago 16, 2010 16:54
- 1 Respostas
- 2350 Exibições
- Última mensagem por MarceloFantini

Ter Ago 17, 2010 00:03
Álgebra Elementar
-
- Raiz quadrada
por anneliesero » Qua Dez 12, 2012 19:26
- 1 Respostas
- 2091 Exibições
- Última mensagem por replay

Qua Dez 19, 2012 16:11
Álgebra Elementar
-
- [raiz quadrada] Ajuda..
por tata545 » Dom Mai 25, 2008 20:45
- 1 Respostas
- 4133 Exibições
- Última mensagem por admin

Dom Mai 25, 2008 21:04
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


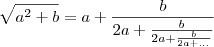
 é o maior número inteiro que ao quadrado não supera o radicando.
é o maior número inteiro que ao quadrado não supera o radicando. é o resto obtido entre o radicando e o valor de
é o resto obtido entre o radicando e o valor de 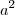 .
. mas com apenas duas frações.
mas com apenas duas frações.  e
e  respectivamente. Então:
respectivamente. Então: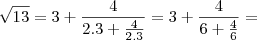
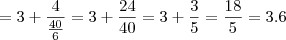 .
.
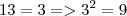 Então 3 é o primeiro algarismo da raiz.
Então 3 é o primeiro algarismo da raiz.