por Danilo » Seg Mar 19, 2012 22:46
por Danilo » Seg Mar 19, 2012 22:46
Considere a desigualdade:
2x - 4/ x + 1 > 1
a questão foi resolvida da seguinte maneira:
Mulplicando-se os dois membros por x+1 obtemos:
2x - 4 > x +1
Somando-se 4 aos dois membros temos:
2x > x + 5
Dimuindo-se x dos dois membros, obtemos finalmente que:
x > 5
Vi alguns erros, mas não sei como colocá-los em ordem no exercício. Me corrijam se eu estiver errado.
primeiro: quem resolveu o problema deveria ter considerado que x + 1 tem que ser diferente de zero, ou seja, maior ou menor. Então, deveria ter considerado os casos em que x+ 1 é positivo, e negativo.
correto?
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Seg Mar 19, 2012 23:20
por MarceloFantini » Seg Mar 19, 2012 23:20
Para evitar erros e perdas de tempo, ao invés de cometer o equívoco clássico de multiplicar por

faça o seguinte:
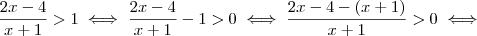
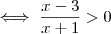
.
Agora analise.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Juvenal » Qua Mar 21, 2012 10:08
por Juvenal » Qua Mar 21, 2012 10:08
Amigos, observem que ficaria para analisar assim:
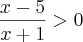
Observem a validação:
1. o resultado é um intervalo de números reais maiores que 5.
2. substitua, na expressão, o X pelo 5, por números maiores que 5 e por números menores que 5 e veja para cada caso quando a expressão é verdadeira.
Contem comigo,
Juvenal
-
Juvenal
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Ter Mar 20, 2012 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharel em Matemática
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Erro na resolução?
por Cleyson007 » Sex Set 21, 2012 16:50
- 1 Respostas
- 1305 Exibições
- Última mensagem por young_jedi

Sex Set 21, 2012 17:53
Cálculo: Limites, Derivadas e Integrais
-
- Identificar funções pares e ímpares
por vmouc » Sex Mar 11, 2011 00:17
- 6 Respostas
- 5531 Exibições
- Última mensagem por vmouc

Sex Mar 11, 2011 19:33
Funções
-
- Como posso Identificar o domínio ?
por Amanda j » Seg Out 24, 2016 12:57
- 0 Respostas
- 3672 Exibições
- Última mensagem por Amanda j

Seg Out 24, 2016 12:57
Cálculo: Limites, Derivadas e Integrais
-
- [Polinômios] como identificar o padrão?
 por Guga1981 » Ter Dez 13, 2016 09:24
por Guga1981 » Ter Dez 13, 2016 09:24
- 4 Respostas
- 11658 Exibições
- Última mensagem por adauto martins

Sex Dez 16, 2016 10:59
Polinômios
-
- Erro ou não?
por R Alvim » Qui Mar 17, 2011 20:10
- 1 Respostas
- 1600 Exibições
- Última mensagem por DanielFerreira

Qua Mar 23, 2011 15:00
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 faça o seguinte:
faça o seguinte: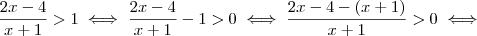
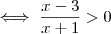 .
.