a) a velocidade na posição C;
b)a tração no fio na posição C;
resposta a ) 3,5
b)7,6 N
eu consigueria fazer a segunda se conseguisse fazer a primeira. pois sei que a tração no ponto mais baixo vai ser a peso + força centrípeta porém não consigo axar a velocidade no primeiro exercício,
No primeiro exercício não consigo é achar a altura A ou B como procedo? coloco na forma da energia mecânica , sabendo que energia potencial em c é nula pois é o ponto mais baixo. e fica
Ecc = Ecb + ecpb ou ecc = epa
não consigo achar nenhuma energia potencial , alguém em ajuda ?

desenho tá um pouco desproporcional,
alguém pode me ajuda ?


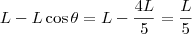 . Usando energia mecânica:
. Usando energia mecânica:
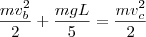
 . Substituindo numericamente, encontramos
. Substituindo numericamente, encontramos 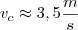 .
.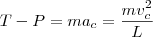 , e assim
, e assim 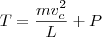 . Substituindo numericamente, encontramos
. Substituindo numericamente, encontramos 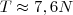 .
.

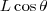 . Assim, a distância menor que está embaixo, que é a que nós queremos, será a altura da posição C menos a altura da posição B.
. Assim, a distância menor que está embaixo, que é a que nós queremos, será a altura da posição C menos a altura da posição B.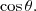
 tal que
tal que  . Seja h o cateto na vertical, então temos
. Seja h o cateto na vertical, então temos 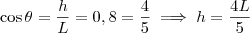 . Tente desenhar e visualizará melhor.
. Tente desenhar e visualizará melhor.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)