-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477883 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 529573 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 493111 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 699225 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2109816 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Jorge Rodrigo » Qui Jun 09, 2011 17:37
por Jorge Rodrigo » Qui Jun 09, 2011 17:37
Boa tarde!
Alguém poderia me ajudar a provar, por indução, a seguinte questão:

Meu desenvolvimento:
Definição:
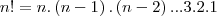

Como viram não consegui igualar os dois membros para poder afirmar a veracidade do PIF para a proposição dada.
-
Jorge Rodrigo
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Mai 18, 2011 18:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Matemática Aplicada
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Princípio da Indução Finita
por Fontelles » Dom Jan 17, 2010 14:42
- 9 Respostas
- 56369 Exibições
- Última mensagem por Vennom

Qui Abr 26, 2012 23:04
Funções
-
- PIF - Principio da Indução Finita
por ederj » Seg Jun 28, 2010 13:35
- 3 Respostas
- 6846 Exibições
- Última mensagem por Tom

Sex Jul 02, 2010 20:01
Funções
-
- Princípio da Indução Finita
por silvia fillet » Qui Out 20, 2011 12:04
- 3 Respostas
- 8062 Exibições
- Última mensagem por silvia fillet

Sex Out 21, 2011 17:33
Álgebra Elementar
-
- [PIF] Princípio de indução finita
por Beckyh » Qua Abr 11, 2012 06:45
- 2 Respostas
- 5101 Exibições
- Última mensagem por Beckyh

Qui Abr 12, 2012 00:21
Funções
-
- [P.I.F]Principio de Indução Finita
por holandaleo » Sáb Fev 13, 2016 18:48
- 1 Respostas
- 3162 Exibições
- Última mensagem por adauto martins

Qui Fev 25, 2016 21:31
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

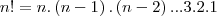



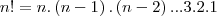


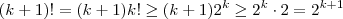




 , avisa que eu resolvo.
, avisa que eu resolvo.

