por hevhoram » Seg Mai 16, 2011 16:59
por hevhoram » Seg Mai 16, 2011 16:59
Uma empresa confeccionou catálogos dos tipos A e B para presentear seus clientes. Um catálogo tipo A pesa 240 g e um do tipo B, 350g. Os catálogos foram organizados em pacotes, contendo cada um deles apenas catálogos de um mesmo tipo.
Com base nas informações do texto, é correto afirmar que, se todos os pacotes tiverem o mesmo peso e se esse peso for inferior a 10kg, então cada pacote pesará
A) 8,2 kg
B) 8,3 kg
C) 8,4 kg
D) 8 kg
E) 8,1 kg
(tentei fazer pelo mdc: mais nao entendi como proceder ????) daí nao sei nem por onde tentar???
-

hevhoram
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qua Jun 02, 2010 11:43
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: informática educacional
- Andamento: formado
 por FilipeCaceres » Seg Mai 16, 2011 17:09
por FilipeCaceres » Seg Mai 16, 2011 17:09
Faça
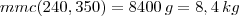
Espero que seja isso.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão fácil, me ajuda, concurso correios 2011 cesp, obriga
por jrmaialds » Seg Nov 12, 2012 16:40
- 2 Respostas
- 2701 Exibições
- Última mensagem por jrmaialds

Seg Nov 12, 2012 18:03
Aritmética
-
- Medida de massa - apostila p/ concurso dos correios
por Igra » Seg Abr 22, 2013 10:49
- 0 Respostas
- 2424 Exibições
- Última mensagem por Igra

Seg Abr 22, 2013 10:49
Conversão de Unidades
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12994 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:21
- 2 Respostas
- 10976 Exibições
- Última mensagem por Elcioschin

Ter Ago 18, 2009 08:54
Progressões
-
- QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:32
- 2 Respostas
- 15117 Exibições
- Última mensagem por GABRIELA

Ter Set 08, 2009 21:21
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.