 por jaquecox » Ter Abr 26, 2011 21:50
por jaquecox » Ter Abr 26, 2011 21:50
oi!! estou há dois dias tentando resolver um problema: o prof. me deu passos que devo seguir:O 1º é:Colocar a interseção maior (no diagrama de venn) mas e quando o examinador quer saber exatamente esse valo? ex: numa pesquisa feita com 400 consumidores sobre a preferencia entre 3 refrigerantes, constatou-se que: 80 pessoas consumiam o tipo a e b . 60 os tipos a e c . 40 os tipos b e c . Entre bos que consumiam apenas um tipo de refrigerante o resultado foi: 200 o tipo a . 150 o tipo b. 170 o tipo c. Sabendo que entre as pessoas pesquisdas , 40 não consomen nenhum dos tres tipos, o número das que consomem os tres tipos é:
eu resolvi esse problema , mas foi quase pelo jogo do bicho, tentando um monte de números ... mas na hora da prova não dá, né? e agora????????????
-
jaquecox
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Abr 26, 2011 21:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Ter Abr 26, 2011 22:52
por FilipeCaceres » Ter Abr 26, 2011 22:52
Uma forma direta de calcular seria,
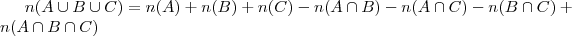
Fazendo
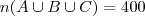
Observe que não retirei os 40 que não tomam nenhum dos 3 refrigerante, logo devemos somar no outro lado também,logo temos,
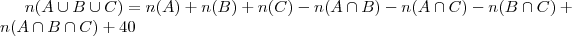
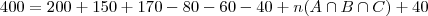
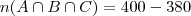

Espero que entenda.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por jaquecox » Qua Abr 27, 2011 08:50
por jaquecox » Qua Abr 27, 2011 08:50
Oi... muito obrigada por ter respondido , eu copiei a fórmula e hoje vou digerí-la até entender.... tenho mais dois exercícios assim tbm, vou tentar resolver... como se faz pra guardar na memória essa fórmula mais fácil, vc tem alguma técnica??? obrigaddaaaaaaaaaaaaaaaaaaaaaaa....
-
jaquecox
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Abr 26, 2011 21:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Qua Abr 27, 2011 09:31
por FilipeCaceres » Qua Abr 27, 2011 09:31
Use o diagrama de Venn.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por jaquecox » Ter Mai 03, 2011 20:56
por jaquecox » Ter Mai 03, 2011 20:56
eu não sei aonde se enquadra essa questão então eu ou perguntar aqui mesmo: ja tentei atéeeeeeeeeeeeee.... já tirei o mmc mas não consigooo..........
a) duas polias conectadas por uma correia tem comprimentos de 12 cm e 22 cm. o menore numero de voltas completas q a polia menor deve dar para que a polia maior de um numero inteoro de voltas é: ??????????
-
jaquecox
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Abr 26, 2011 21:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Ter Mai 03, 2011 21:14
por FilipeCaceres » Ter Mai 03, 2011 21:14
Nunca utilize um tópico para postar uma outra questão é muito melhor que você crie em um lugar errado um novo que utilize um antigo.
Espero que alguém consiga trocar de lugar.
Solução:
Faça o mmc deles.
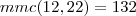
A quantidade mínima de voltas completas é:
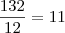
voltas
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Conjuntos] Exercício de conjuntos com áreas
 por redleader » Ter Abr 02, 2013 16:12
por redleader » Ter Abr 02, 2013 16:12
- 0 Respostas
- 1549 Exibições
- Última mensagem por redleader

Ter Abr 02, 2013 16:12
Conjuntos
-
- Exercício de Conjuntos
por Loretto » Seg Out 11, 2010 18:26
- 0 Respostas
- 1316 Exibições
- Última mensagem por Loretto

Seg Out 11, 2010 18:26
Álgebra Elementar
-
- Exercício de conjuntos
 por LuizCarlos » Dom Jun 17, 2012 15:25
por LuizCarlos » Dom Jun 17, 2012 15:25
- 2 Respostas
- 2346 Exibições
- Última mensagem por skin

Dom Jul 15, 2012 23:24
Conjuntos
-
- Duvida em exercicio de Conjuntos
por krobc » Sáb Mar 17, 2012 12:07
- 0 Respostas
- 1183 Exibições
- Última mensagem por krobc

Sáb Mar 17, 2012 12:07
Conjuntos
-
- [Conjuntos] Dúvidas no exercício.
por HeidyTrinidad » Sex Abr 11, 2014 10:35
- 1 Respostas
- 1805 Exibições
- Última mensagem por e8group

Sex Abr 11, 2014 18:16
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


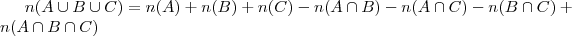
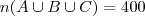
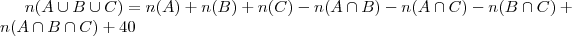
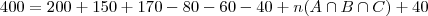
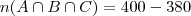


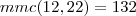
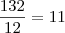 voltas
voltas![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)