-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478840 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 536019 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 499690 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 717929 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2142974 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por juliomarcos » Dom Set 14, 2008 00:46
por juliomarcos » Dom Set 14, 2008 00:46
Prove que todo corpo é domínio de integridade:
Definições do livro do Castrucci:
Um corpo é um anel com elemento unidade 1, onde todo elemento -{0}(elemento neutro da +) possui inverso.
Um domínio de integridade (ou anel de integridade) é um anel comutativo(vale a comutatividade na segunda operação(1) ) com elemento unidade e não possui divisores próprios do zero(2).
Todo corpo é domínio de integridade. Prova:
Seja C um corpo. Como vale o elemento inverso em C, a.a'=a'.a=1, logo também vale a comutatividade para a segunda operação. (1)
Suponha por absurdo que 0 tem inverso.
0.0'=1
0.0' + 0 = 1 + 0
0.(0' + 0) = 1
0 = 1
Absurdo, já que 0 é diferente de 1, logo 0.0'

1 ou 0.0' = 0, mas como 0' não existe em C, 0 não tem divisores próprios.(2)
Algum perito em teoria dos conjuntos pode corrigir isto pra mim? Grato.
-
juliomarcos
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Dom Set 14, 2008 00:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por admin » Qua Set 17, 2008 04:04
por admin » Qua Set 17, 2008 04:04
Olá
juliomarcos, boas-vindas!
Assumo uma modesta postura de aluno, tanto é que minha atual formação está longe de sanar dúvidas da graduação de um modo geral.
Ainda assim, acredito que sua suposição por absurdo deva ser outra.
Como queremos mostrar que os elementos do corpo não possuem divisores de zero, supomos por absurdo que eles possuem.
Eis uma demonstração de uma das minhas aulas em Álgebra II, também encontrada em alguns livros.
Adicionei alguns comentários:
Suponha por absurdo que existam
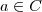
,
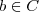
tais que
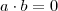
e

e

Note acima que esta suposição é equivalente a dizer que
 não
não é um domínio e ainda

e
 são
são divisores de zero!
Como

é corpo e

, existe
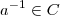
tal que
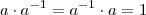
Então
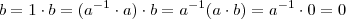
juliomarcos, veja um destaque sobre o absurdo: inicialmente havia a suposição de que

.
Como concluímos que

, então
 não
não é divisor de zero!
E pela definição de domínio de integridade:
Seja

um anel comutativo com unidade.
Dizemos que A é um anel de integridade ou domínio de integridade ou simplesmente domínio se A satisfaz a seguinte condição:
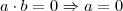 ou
ou 
Ou seja, como

,

é um domínio, pois
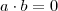
por hipótese!
Espero ter ajudado.
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 886
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por juliomarcos » Qua Set 17, 2008 11:16
por juliomarcos » Qua Set 17, 2008 11:16
Obrigado pela resposta e pelas boas-vindas. Só mais uma coisa. Posso afirmar que todo anel com elemento unidade é um anel comutativo?
Gostaria de saber "qual" definição de Corpo você usou. Estou dizendo isso porque no livro "Curso de Álgebra vol1" de Ábramo Hefez, a comutatividade da segunda operação está definida pra qualquer anel, já no livro do Castrucci, um anel que goze da comutatividade na segunda operação é chamado anel comutativo. O resto da prova eu entendi. Muito obrigado.
-
juliomarcos
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Dom Set 14, 2008 00:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por admin » Ter Set 23, 2008 17:22
por admin » Ter Set 23, 2008 17:22
Olá
juliomarcos, boa-tarde!
juliomarcos escreveu:Posso afirmar que todo anel com elemento unidade é um anel comutativo?
Não. Um contra-exemplo é o anel
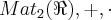
(o conjunto de todas as matrizes reais 2x2). Cuja unidade é:
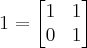
Este anel não é comutativo.
juliomarcos escreveu:Gostaria de saber "qual" definição de Corpo você usou.
Sobre a definição de corpo, citarei duas que usei, uma dada em aula, cuja bibliografia indicarei em seguida:
Definição: Um anel comutativo com unidade é chamado de corpo se todo elemento
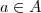
,

, é inversível (isto é, existe
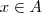
tal que

).
Notação:

é único e indicado por

.
Bibliografia do curso:
1. Herstein, I.N., "Topics in Algebra", 2nd Edition, John Wiley & Sons (tem tradução).
2. Dean, R.A., "Elements of Abstract Algebra", Wiley International Edition, John Wiley and Sons.
3. Gonçalves, A., "Introdução à Álgebra", IMPA.
4. Lang, S., "Algebraic Structures", Addison - Wesley Publishing Company (tem tradução).
5. Fraleigh, J.B., "A first course in abstract algebra", Addison Wesley.
Eu tenho o livro do Adilson, o 3º da lista, cuja definição é a seguinte:
Definição: Se um domínio de integridade
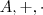
satisfaz a propriedade:
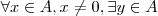
tal que
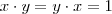
,
dizemos que
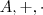
é um
corpo.
Lembrando que antes há a seguinte definição para domínio de integridade:
Se
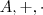
é um anel comutativo, com unidade e sem divisores de zero, dizemos que
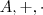
é um
domínio de integridade.
Até mais!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 886
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por juliomarcos » Qua Set 24, 2008 01:03
por juliomarcos » Qua Set 24, 2008 01:03
Agora e depois de ter tirado umas dúvidas com a professora, compreendi totalmente o assunto. Muito Obrigado.
-
juliomarcos
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Dom Set 14, 2008 00:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Leis do Cancelamento em Domínios de Integridade
por m0x0 » Sáb Jul 23, 2011 20:18
- 0 Respostas
- 1660 Exibições
- Última mensagem por m0x0

Sáb Jul 23, 2011 20:18
Álgebra Elementar
-
- Corpo
por GehSillva7 » Qui Fev 25, 2016 12:55
- 2 Respostas
- 1550 Exibições
- Última mensagem por GehSillva7

Dom Fev 28, 2016 15:40
Aritmética
-
- Trabalho e potência de um corpo
por HenriqueGS » Dom Jul 09, 2017 18:20
- 0 Respostas
- 1664 Exibições
- Última mensagem por HenriqueGS

Dom Jul 09, 2017 18:20
Física
-
- Derivada Corrijam por favor
por costav13 » Seg Out 28, 2013 12:03
- 2 Respostas
- 1445 Exibições
- Última mensagem por costav13

Sáb Nov 02, 2013 19:58
Cálculo: Limites, Derivadas e Integrais
-
- Derivada Corrijam por favor
por costav13 » Seg Out 28, 2013 18:12
- 1 Respostas
- 1073 Exibições
- Última mensagem por Taka

Sáb Nov 02, 2013 16:53
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 46 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 1 ou 0.0' = 0, mas como 0' não existe em C, 0 não tem divisores próprios.(2)
1 ou 0.0' = 0, mas como 0' não existe em C, 0 não tem divisores próprios.(2)

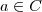 ,
, 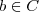 tais que
tais que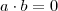 e
e  e
e 

 e
e 
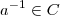 tal que
tal que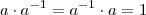
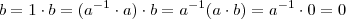
 , então
, então  um anel comutativo com unidade.
um anel comutativo com unidade.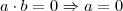

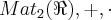 (o conjunto de todas as matrizes reais 2x2). Cuja unidade é:
(o conjunto de todas as matrizes reais 2x2). Cuja unidade é: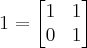
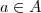 ,
, 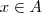 tal que
tal que  ).
). é único e indicado por
é único e indicado por  .
.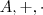 satisfaz a propriedade:
satisfaz a propriedade: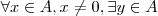 tal que
tal que 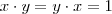 ,
, } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: