-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478481 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 533105 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 496617 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 709425 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2128005 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Abelardo » Sáb Mar 12, 2011 16:54
por Abelardo » Sáb Mar 12, 2011 16:54
Seja p o maior fator primo do número
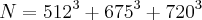
. A soma dos algarismos de p é igual a:
a) 13
b) 14
c) 15
d) 16
e) 17
Fatorei as parcelas e depois tentei isolar alguns termos, mas no final fico com duas parcelas com expoentes estratosféricos! Alguma
DICA!
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Sáb Mar 12, 2011 19:48
por LuizAquino » Sáb Mar 12, 2011 19:48
De que ano é esse exercício da OBM?
Na página oficial da OBM podemos acessar todas as provas e gabaritos (com resolução). Visite:
http://www.obm.org.br
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Abelardo » Sáb Mar 12, 2011 22:04
por Abelardo » Sáb Mar 12, 2011 22:04
Professor Aquino, essa questão e outras são parte do programa da própria OBM. Recebo por email algumas questões para solucioná-las e posso enviar questões para que outros! Estou respondendo as provas mais antigas e sempre que travo em alguma coisa venho aqui no ajudamatematica e consigo desenvolver o resto!
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Dom Mar 13, 2011 03:26
por MarceloFantini » Dom Mar 13, 2011 03:26
Talvez quem saiba teoria dos números possa usar algum teorema ou raciocínio de congruência, acho que seja um caminho, porque fatorar está complicado.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Abelardo » Dom Mar 13, 2011 13:26
por Abelardo » Dom Mar 13, 2011 13:26
Pensei também na possibilidade de alguma técnica de congruência. Vou procurar nos arquivos da OBM alguns artigos que falem de congruência, aposto que deve ter algum exercício similar! Obrigado Fantini, estou mais confiante nisso.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Teoria Números] Algoritmo Não Interceptação Números Primos
por WillamesSilva » Qua Out 26, 2016 12:21
- 8 Respostas
- 14970 Exibições
- Última mensagem por WillamesSilva

Ter Nov 22, 2016 15:33
Aritmética
-
- Números primos
 por mony0771 » Qui Abr 23, 2009 10:54
por mony0771 » Qui Abr 23, 2009 10:54
- 2 Respostas
- 2827 Exibições
- Última mensagem por mony0771

Qui Abr 23, 2009 15:28
Álgebra Elementar
-
- Numeros Primos
por Neperiano » Sex Abr 24, 2009 20:15
- 6 Respostas
- 3938 Exibições
- Última mensagem por Neperiano

Sáb Abr 25, 2009 10:23
Problemas do Cotidiano
-
- Números Primos
por Abelardo » Qua Mar 09, 2011 21:38
- 1 Respostas
- 1862 Exibições
- Última mensagem por Abelardo

Qua Mar 09, 2011 21:41
Álgebra Elementar
-
- Números primos!
por Abelardo » Dom Mar 13, 2011 00:24
- 1 Respostas
- 1308 Exibições
- Última mensagem por Renato_RJ

Dom Mar 13, 2011 01:00
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 16 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
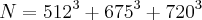 . A soma dos algarismos de p é igual a:
. A soma dos algarismos de p é igual a:
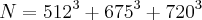 . A soma dos algarismos de p é igual a:
. A soma dos algarismos de p é igual a:







 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.