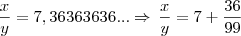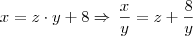por Abelardo » Qui Mar 10, 2011 13:45
por Abelardo » Qui Mar 10, 2011 13:45
45. Considere x, y e z números naturais. Na divisão de x por y obtém-se quociente z e resto 8. Sabe-se que a representação decimal de

é a dízima periódica 7,363636... Então, o valor de x + y + z é:
a)190
b)193
c)191
d)192
Só encontro 190 como resposta, mas a resposta é 191! Alguma luz, não quero que resolvam para mim, quero alguma dica.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Renato_RJ » Qui Mar 10, 2011 15:03
por Renato_RJ » Qui Mar 10, 2011 15:03
Abelardo, vamos ver esse problema...
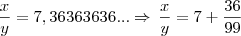
Sabemos que:
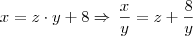
Agora, faça a substituição e veja o resultado, é 191 mesmo...
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Abelardo » Sex Mar 11, 2011 22:27
por Abelardo » Sex Mar 11, 2011 22:27
Caramba, deixei a geratriz na forma de fração irredutível e nem me toquei que poderia destrinchá-la !! Valeu mesmo, consegui.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Renato_RJ » Sáb Mar 12, 2011 00:48
por Renato_RJ » Sáb Mar 12, 2011 00:48
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Conjuntos numéricos
por Marcampucio » Ter Set 01, 2009 21:50
- 1 Respostas
- 1446 Exibições
- Última mensagem por Elcioschin

Ter Set 01, 2009 22:38
Álgebra Elementar
-
- Conjuntos numericos
por cristina » Seg Set 14, 2009 18:41
- 1 Respostas
- 1629 Exibições
- Última mensagem por Molina

Ter Set 15, 2009 16:07
Álgebra Elementar
-
- CONJUNTOS NUMÉRICOS
por shallon » Qua Out 28, 2009 23:38
- 0 Respostas
- 1218 Exibições
- Última mensagem por shallon

Qua Out 28, 2009 23:38
Álgebra Elementar
-
- CONJUNTOS NUMÉRICOS
por shallon » Qua Out 28, 2009 23:40
- 0 Respostas
- 1253 Exibições
- Última mensagem por shallon

Qua Out 28, 2009 23:40
Álgebra Elementar
-
- CONJUNTOS NUMÉRICOS
por shallon » Qua Out 28, 2009 23:42
- 0 Respostas
- 1054 Exibições
- Última mensagem por shallon

Qua Out 28, 2009 23:42
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é a dízima periódica 7,363636... Então, o valor de x + y + z é:
é a dízima periódica 7,363636... Então, o valor de x + y + z é:
 é a dízima periódica 7,363636... Então, o valor de x + y + z é:
é a dízima periódica 7,363636... Então, o valor de x + y + z é: