-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480161 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 539090 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 502969 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 726211 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2161929 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Abelardo » Seg Mar 07, 2011 00:50
por Abelardo » Seg Mar 07, 2011 00:50
(PUC-RJ) Ache dois divisores diferentes, entre 60 e 70, do número
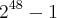
.
Estou estudando sobre números primos e há um tópico especial falando sobre os ''números de Mersenne''. Como o a base é 2, o seu resultado é par, mas tem a subtração que o torna um número impar..
pensei em fatorá-lo, mas não vi como. Pensei em um produto notável, mas não tem ''futuro prático'', ficaria inúmeros fatores.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Renato_RJ » Seg Mar 07, 2011 15:33
por Renato_RJ » Seg Mar 07, 2011 15:33
Boa tarde Abelardo..
Vou dar uma dica:
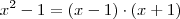
Olha o que aconteceu com a potência de x....
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Abelardo » Seg Mar 07, 2011 18:47
por Abelardo » Seg Mar 07, 2011 18:47
sei que é dividido por dois quando desenvolvemos a diferença de dois quadrados... mas e a partir dai, devo continuar com o desenvolvimento de (

?
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Renato_RJ » Seg Mar 07, 2011 18:57
por Renato_RJ » Seg Mar 07, 2011 18:57
Boa tarde Abelardo, vamos lá...
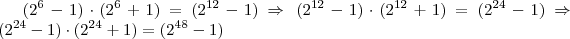
Arrumando tudo temos:

Como

sabemos que os dois divisores que se encontram no intervalo dado só podem ser
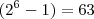
e
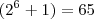
.
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Abelardo » Seg Mar 07, 2011 20:14
por Abelardo » Seg Mar 07, 2011 20:14
Valeu Renate, você sempre respondendo as minhas perguntas! Brigadão mesmo..
Consegui chegar a solução, incrivelmente (pelo menos para mim) enquanto ia comprar o pão e estava andando de bicicleta.. lembrei da fórmula para números ímpares e de que entre um par há dois primos. Já que a expressão dada é um número ímpar, então entre 60 e 70 tenho 64 como potência de 2, logo posso ter 64+1=65(ímpar) e 64-1=63(ímpar).
Valeu cara!
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- determinação de ponto
por wanderley argenton » Seg Mai 28, 2012 13:58
- 1 Respostas
- 2979 Exibições
- Última mensagem por LuizAquino

Seg Mai 28, 2012 17:42
Geometria Analítica
-
- Determinação de um plano
 por ViniciusAlmeida » Sex Mai 29, 2015 00:07
por ViniciusAlmeida » Sex Mai 29, 2015 00:07
- 0 Respostas
- 1013 Exibições
- Última mensagem por ViniciusAlmeida

Sex Mai 29, 2015 00:07
Geometria Analítica
-
- Determinação de domínio da função
por Jonatan » Qua Jul 28, 2010 13:24
- 1 Respostas
- 2904 Exibições
- Última mensagem por MarceloFantini

Qua Jul 28, 2010 14:51
Funções
-
- demonstração e determinação de raizes
por tigre matematico » Sáb Out 15, 2011 23:29
- 0 Respostas
- 789 Exibições
- Última mensagem por tigre matematico

Sáb Out 15, 2011 23:29
Polinômios
-
- [Determinaçao do Momento-Inequaçoes]
por R0nny » Sex Mai 03, 2013 15:12
- 10 Respostas
- 4373 Exibições
- Última mensagem por e8group

Sáb Mai 04, 2013 15:53
Inequações
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
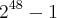 .
. 

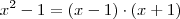
 ?
?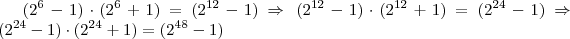

 sabemos que os dois divisores que se encontram no intervalo dado só podem ser
sabemos que os dois divisores que se encontram no intervalo dado só podem ser 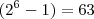 e
e 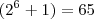 .
.
 .
.



