 N / k < x <
N / k < x <![\sqrt[]{5} \sqrt[]{5}](/latexrender/pictures/0be1c4ad0f7708e4012e708b953ffd6c.png) } onde k é a solução
} onde k é a solução 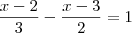 , B = [m,n[, onde m e n são raízes da equação x² - 2x – 15= 0, C = {0}
, B = [m,n[, onde m e n são raízes da equação x² - 2x – 15= 0, C = {0}  [2,7[ e D = {x
[2,7[ e D = {x  R/
R/ 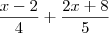 < 5}
< 5}Determine (D - ?)
 (C
(C  B)
B)Eu encontrei:
A = ]-1, 2]
B = [-5,3[
C = {0,2,3,4,5,6}
D = ]-
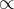 , 6]
, 6]
 N / k < x <
N / k < x <![\sqrt[]{5} \sqrt[]{5}](/latexrender/pictures/0be1c4ad0f7708e4012e708b953ffd6c.png) } onde k é a solução
} onde k é a solução 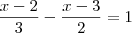 , B = [m,n[, onde m e n são raízes da equação x² - 2x – 15= 0, C = {0}
, B = [m,n[, onde m e n são raízes da equação x² - 2x – 15= 0, C = {0}  [2,7[ e D = {x
[2,7[ e D = {x  R/
R/ 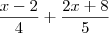 < 5}
< 5} (C
(C  B)
B)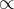 , 6]
, 6]
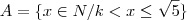 onde k é a solução
onde k é a solução 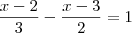
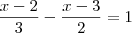
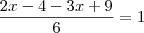
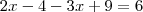
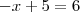

 são naturais maiores do que -1 e menores do que raiz de 5, temos que:
são naturais maiores do que -1 e menores do que raiz de 5, temos que: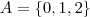
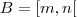 , onde m e n são raízes da equação
, onde m e n são raízes da equação 
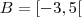
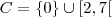
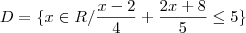
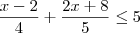
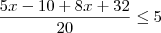
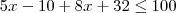
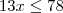

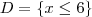


Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

