a questão é a seguinte.
Use a definição de valor absoluto e reescreva as expressoões a seguir sem usas o símbolo de valor absoluto.
 eu fiz assim:
eu fiz assim:
em uma outra e fiz assim.
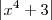
![{x}^{4}+3=0 \Rightarrow {x}^{4}=-3 \Rightarrow x=-+\sqrt[4]{-3} {x}^{4}+3=0 \Rightarrow {x}^{4}=-3 \Rightarrow x=-+\sqrt[4]{-3}](/latexrender/pictures/1d694a7cf1102cb754a9434fb50f0c8e.png)
está correto as respostas?

 eu fiz assim:
eu fiz assim:
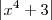
![{x}^{4}+3=0 \Rightarrow {x}^{4}=-3 \Rightarrow x=-+\sqrt[4]{-3} {x}^{4}+3=0 \Rightarrow {x}^{4}=-3 \Rightarrow x=-+\sqrt[4]{-3}](/latexrender/pictures/1d694a7cf1102cb754a9434fb50f0c8e.png)


 ). Já o módulo de -19 é 19 (simbolicamente:
). Já o módulo de -19 é 19 (simbolicamente: 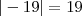 ).
).
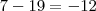
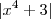 perceba que este valor que está dentro do módulo será sempre positivo, independente do x que eu pegar, pois
perceba que este valor que está dentro do módulo será sempre positivo, independente do x que eu pegar, pois 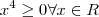 .
.

 se x<7
se x<7 
jose henrique escreveu:entãose x<7
-x+7
neste caso estaria correto?



Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)