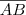por Balanar » Dom Ago 29, 2010 19:55
por Balanar » Dom Ago 29, 2010 19:55
Sejam M e N os pontos médios, respectivamente, dos segmentos
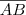
e

, contidos numa mesma reta, sendo

, com

.
Demonstre que

é congruente a
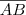
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Guill » Dom Jul 03, 2011 17:45
por Guill » Dom Jul 03, 2011 17:45
O segmento AB é congruente ao segmento BC. Se M é ponto médio de AC e N é ponto médio de BC:
AM = MB e BN = NC
Sabe-se que AB = BC. Logo:
AM = MB = BN = NC
Considerando que MB tenha um comprimento x,
AM = x
MB = x
BN = x
NC = x
Determinamos, então que AB = 2x pois M é ponto médio.
Podemos considerar que b é ponto médio de MN pois, MB = BN. Sendo assim:
MN = 2x
Concluimos então que AB = MN
-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Congruência
por ronie_mota » Dom Set 27, 2009 16:59
- 1 Respostas
- 1793 Exibições
- Última mensagem por Molina

Seg Set 28, 2009 16:15
Álgebra Elementar
-
- Congruência!
por Abelardo » Dom Abr 10, 2011 01:03
- 2 Respostas
- 1914 Exibições
- Última mensagem por Abelardo

Dom Abr 10, 2011 01:39
Álgebra Elementar
-
- congruência
por hatsurei » Ter Set 13, 2011 11:09
- 1 Respostas
- 7866 Exibições
- Última mensagem por ronaldoh

Qui Jan 05, 2012 17:26
Álgebra Elementar
-
- Divisibilidade, congruência
por ckde » Seg Ago 02, 2010 10:42
- 0 Respostas
- 1199 Exibições
- Última mensagem por ckde

Seg Ago 02, 2010 10:42
Álgebra Elementar
-
- Congruência e Divisibidade
por fernando_filho » Qua Jun 26, 2013 19:52
- 0 Respostas
- 979 Exibições
- Última mensagem por fernando_filho

Qua Jun 26, 2013 19:52
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
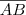 e
e  , contidos numa mesma reta, sendo
, contidos numa mesma reta, sendo  , com
, com  .
.  é congruente a
é congruente a 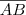

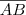 e
e  , contidos numa mesma reta, sendo
, contidos numa mesma reta, sendo  , com
, com  .
.  é congruente a
é congruente a