Olá Cleyson.
A idéia principal é considerar o fato de que em cada dia há uma quantidade diferente de capim que cresce constantemente.
Em seguida, precisamos calcular quantas vacas comeriam toda esta quantidade de capim, em cada dia considerado.
Veja a representação desta idéia:
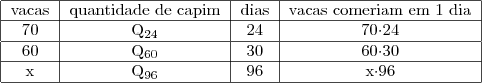
Onde
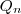
é a quantidade momentânea de capim no dia

.
Sobre a 4ª coluna: o número de vacas (1ª coluna) e o número de dias que dura o pasto (3ª coluna), são inversamente proporcionais em cada linha, ou seja, se multiplicarmos um, o outro deve ser dividido na mesma proporcão. Por isso que para encontrarmos o valor da 4ª coluna, fizemos uma conta intermediária que foi dividir o número da 3ª coluna pelo seu próprio valor, para obtermos 1 dia. Sendo assim, o número de vacas (1ª coluna) é multiplicado pelo valor correspondente cujo produto consta na 4ª coluna.
Exemplo da 1ª linha:
dividimos o número de dias que dura o pasto por 24, para então termos 1 dia. Então, o número de vacas que comerão aquela quantidade fixada de capim
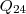
deverá ser o valor anterior
multiplicado por 24.
Reescrevendo:
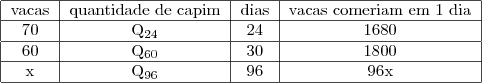
Agora, é preciso representar a quantidade
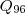
através das quantidades
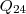
e

.
Podemos fazer a diferença
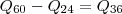
e somar com

.
Resumindo,
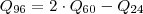
.
Então, também representamos o número de vacas que comeriam esta quantidade
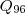
em 1 único dia:
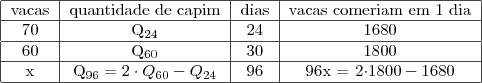
Da equação da última célula, calculamos o valor de

que é o número de vacas que comeriam a quantidade
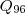
de capim em
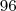
dias.
Espero ter ajudado!



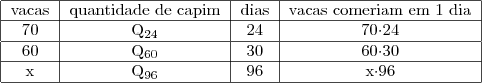
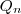 é a quantidade momentânea de capim no dia
é a quantidade momentânea de capim no dia  .
.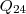 deverá ser o valor anterior
deverá ser o valor anterior 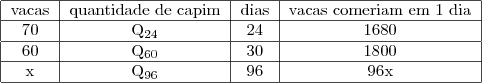
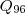 através das quantidades
através das quantidades  .
.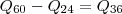 e somar com
e somar com 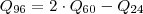 .
.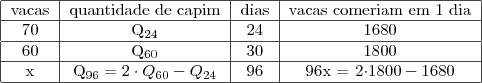
 que é o número de vacas que comeriam a quantidade
que é o número de vacas que comeriam a quantidade 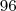 dias.
dias.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.